本文来自Chem-Station日文版 化学者だって数学するっつーの! :定常状態と変数分離 やぶ
翻译投稿 炸鸡 校对 HaoHu
本篇内容旨在介绍为了求解电子安定在原子轨道或分子轨道时电子的波函数而存在的“与时间无关的薛定谔方程”。本次内容将带来求解偏微分方程的技巧——变量分离,同时会介绍驻波是什么,解释为什么会假定波函数表示的是驻波。
上期回顾:薛定谔方程的推导
在上一回里,我们用微分的数学手段将粒子性和波动性相联系,导出了薛定谔方程。方式形如下:
等等!这个方程和大学教材上写的方程怎么不太一样啊?!
我们推导出来的薛定谔方程的正式名称叫做“有关时间的薛定谔方程”。因为是“关于时间的”,所以我们能自然而然知道方程的解(即波函数)会随着时间变化。但是很多大学本科的物理化学,无机化学,有机化学等教材上的薛定谔方程却是“与时间无关的薛定谔方程”。
我们来比较一下两种不同的薛定谔方程,一个是不关于时间的,另一个是关于时间的。包含粒子位置的偏微分(Δ)的等式左边差别不大,但是等式右边却差别很大。不关于时间的薛定谔方程的右边是粒子能量E(为定数)与波函数的乘积。并且波函数的变量只有表示粒子位置的变量(r),并没有出现时间t。仿佛时间在这个方程里凝固了。总之从这个方程里是没有获得与时间有关的任何信息。
目前,让我们导出与时间无关的薛定谔方程,然后再考虑该方程的含义。
不关于时间的薛定谔方程是怎么推导出来的呢?
假定波函数表示的是驻波再通过分离变量就得到了不关于时间的薛定谔方程。下面让我们顺次来看。
Step1:假定波函数表示的是驻波
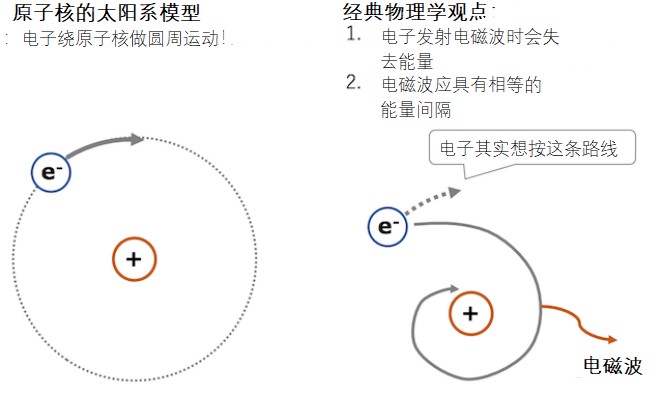
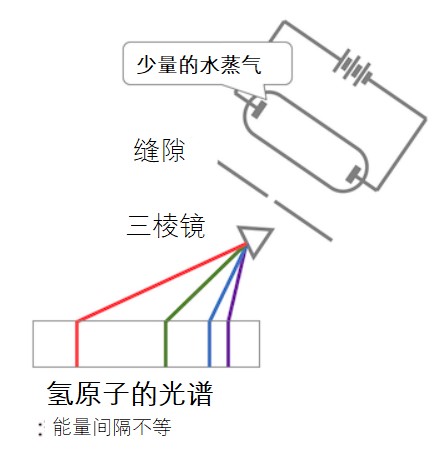
还记得高中物理上那个我们熟悉的原子模型的发展历史吗?传统物理学得出的结论是,当带电粒子做圆周运动时,它会辐射电磁波,从而失去能量并最终落入原子核。换句话说,按照经典物理学,原子核将无法稳定地存在。经典物理学还提出带电粒子进行圆周运动时发出的电磁波应具有相等的能量间隔。但是,当实际观察到氢原子发出的光时,能量间隔是不相等的,如下图所示。
古典物理学和原子结构的不合理性。如果电子的运动遵循经典的物理学定律,那么太阳系模型的原子核将具有非常短的寿命
氢原子的光谱。在内含有少量水蒸气的管两端加上电压,产生了由于水的离解而产生的氢原子和OH–。由于OH–的发出的光不在可见光范围内,因此只能观察到氢原子发出的光。这些光透过棱镜后,组成光的电磁波就会按照波长被分离开来。结果发现发射的光(即氢原子发出的光)仅由遵循一定定律的波长的光波组成
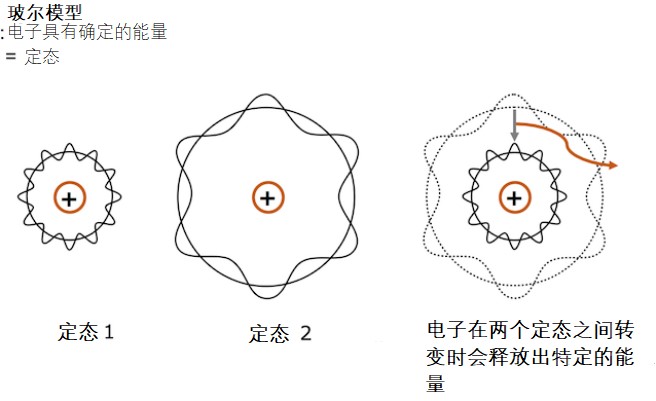
为了解释这一现象,玻尔设想原子中的电子具有的能量是确定的。所以我们把粒子处于这样的能量状态称为“定态”。定态的意思是只要处于这种状态,电子就是稳定的并且不会辐射电磁波。
玻尔推测氢原子光谱是因为电子转移到了不同的定态所造成的
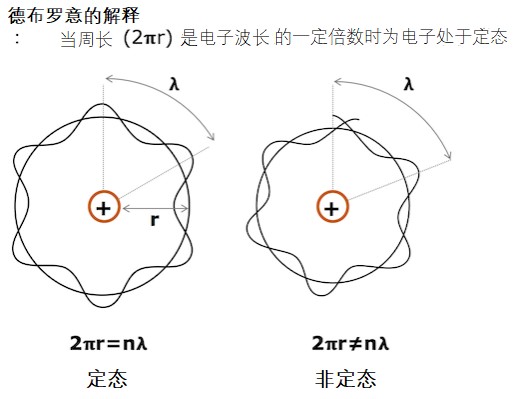
之后德布罗意提出了电子波这一概念,指出定态应理解为电子波围绕核形成驻波的一种状态。即:当电子围绕原子核作圆周运动时,如果其运动周长是电子波波长的整数倍,那么这个电子就是稳定的。
德布罗意的驻波解释。只有当电子的运动周长为电子波波长的整数倍时,驻波才会形成。若电子波的波长部位运动周长的整数倍,第一圈,第二圈和第三圈的波会相互抵消
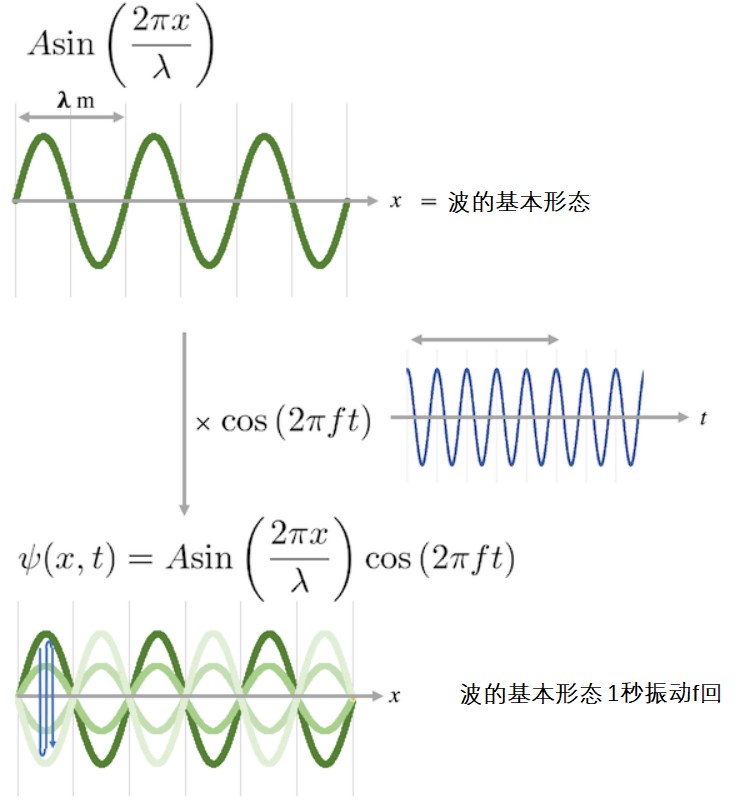
让我们把驻波这一概念融入到薛定谔方程吧。假定波函数表示的波是驻波,那么可以用如下函数表示波函数。
可以看到sin函数部分的变量只有代表粒子位置的x。然而,cos函数的变量只有时间t。ψ波由sin函数确立波的基本形态,ψ波根据时间沿竖直方向重复做伸缩运动。换句话说,波形本身不会向前或向后移动,如下图所示。
一种驻波函数
现在我们改用下面的一般形式表示驻波波函数。
Step2:将驻波函数带入薛定谔方程。
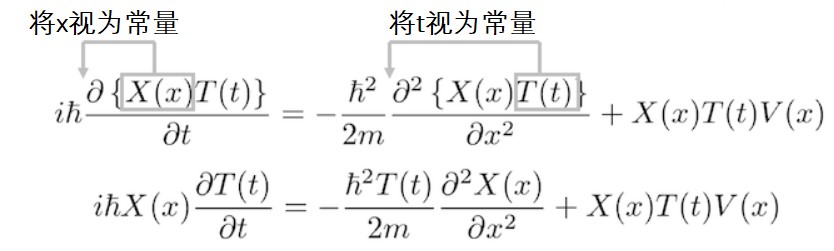
将先前假设的驻波的函数带入到薛定谔方程中。由于带入3维薛定谔方程有一定难度,故选择带入一维薛定谔方程。让我们在一维薛定谔方程中考虑势能只与x有关的系统。
带入后我们可以看到等式左边是关于时间的一个偏微分,只有与时间有关的函数 T (t)在真正发挥作用(此处不明白的同学可参考偏导数的定义。二元函数z=f(x,y),如果只有自变量x变化,而自变量y固定,即视y为常量,这是z就是x的一元函数,z对x的导数就称为二元函数z=f(x,y)对于x的偏导数。)位置函数X (x)提到外面。同理,等式右边里的时间T (t)也提到外面。
Step3:两边变量分离
等式两边同时除以T(t) X(x)。那么等式左边之前提出来的X(x)可以约分掉。但是请注意,T(t) 不可以被约分掉。T(t)可以通过后面的微分操作变形。比如T(t)= cosωt,T(t)对时间求导,得到 –ωsin ωt 。当然sin函数不能被cos函数约分掉的。右边亦是同理,T(t)可以被约分掉,但X(x) 要保留。
最后,等式左边的变量只有时间t,等式右边的变量只有位置(x)。我们需要思考不同变量的两个函数相等是怎么一回事呢?t,x本是毫无关系的两个变量,为什么两个函数竟然能相等呢?解开谜题的关键在于“这两个函数实际上都没有发生变化且值相等”。让我们暂且将该值定义为E。虽然用别的大写字母比如A,C也行,但是你稍后会明白为什么这里要用E。
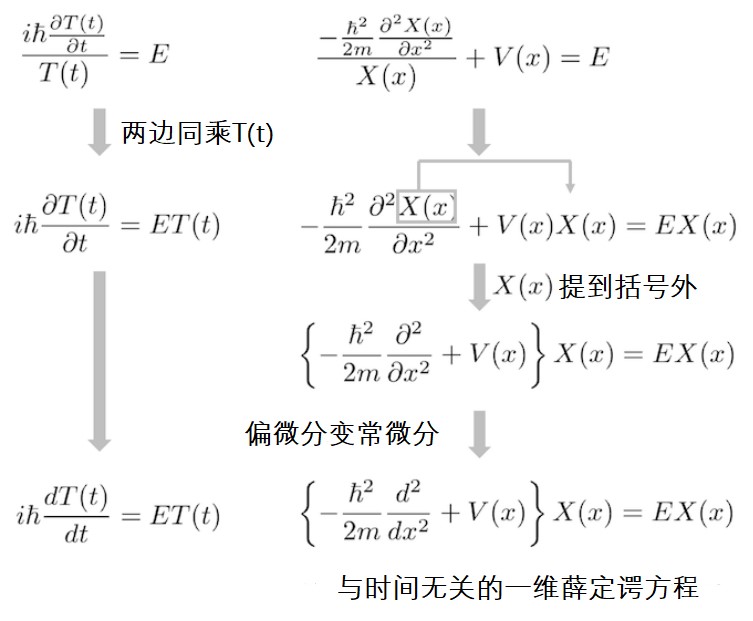
这样我们就得到了不关于时间的薛定谔方程和关于时间的薛定谔方程。现在的方程求微分不需要求偏微分,因为求偏微分是当函数有两个以上变量时,对其中一个变量求微分而把另一个变量当作常数的操作,现在的函数里只有一个变量。现在我们把被微分的函数分开来,用微分形式来代替偏微分形式。
如上,我们就推导出了不关于时间的一维薛定谔方程。将其扩展到3维空间就得到了化学教材上的薛定谔方程了。
推导出来的方程式能简单地求得解吗?
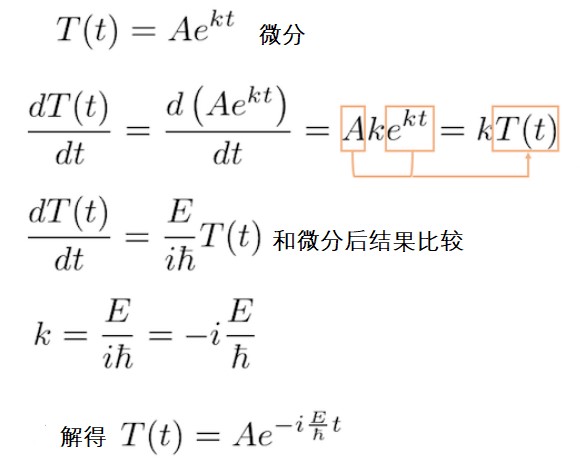
关于时间的薛定谔方程能立即求解。我们需要思考的是有没有一个函数,它求一阶微分再乘以一定常数后得到的是的整数倍(E倍)的原函数。这样性质的函数就是指数函数(小伙伴们有没有想到呢?)!为了适应含虚数的系数,稍微调整下指数函数的指数部的系数即可求得方程的解。
有个复数指数函数的解意味着什么呢?
驻波意味着其绝对值随时间恒定,并且只有复数的相位旋转。把方程的解带入定态的波函数中详细说明下吧。
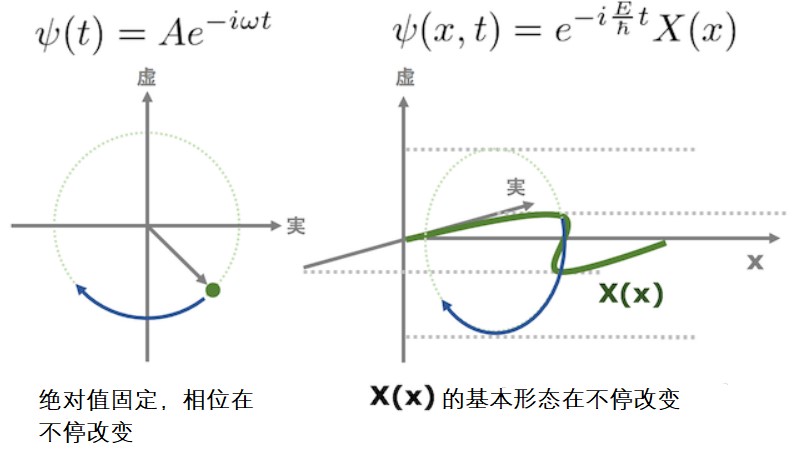
正如笔者在前一篇文章中提到的,以虚数i为指数的指数函数是一个绝对值恒定的函数,并且只有复数平面中的相位随着t的变化而旋转。将这个概念扩展一下,波函数ψ(x,t)是“波的基本形状由X(x)确定,并且基本形状使每个坐标的绝对值保持恒定”的函数。这就是驻波的性质。限于篇幅不会在本文中详细介绍了,但波函数平方的绝对值表示粒子存在的概率,因此绝对值不变的事实在物理上非常重要。
复数指数函数的指数改变,但方程的绝对值不变。改变的只有相位
怎么求解关于位置的方程呢?
和上一个方程的求解比起来这个方程的求解要困难很多。让我们再仔细看一下先前求得的不关于时间的薛定谔方程吧。等式右边,我们看到V(x)是系统的势能,E和V(x)可以相加和相减。这一点意义很重大。之前我们令这个方程等于一个值时曾将这个值设为E,实际上E和V(x)单位一样。也就是说E表示的是能量。
在上一篇里我们对波函数求关于x的二阶微分,求得二阶微分再乘以系数后的结果是一个有关动能的表达式。因此,我们可以知道E是动能和势能的和,即粒子的总能量。所以我们思考有没有一个函数,求它的二阶微分后乘以系数加上势能函数,这个和与函数的乘积等于粒子总能量倍的函数?
如果将其应用于未知系统(例如氢原子)并求解,则可以获得系统的波函数和能量E。但是求得这个方程在数学上是非常困难的。原因是如果变量x包含在势能函数中,则不能像前面的示例中那样求得它是“直观的指数函数”。当然对于不同的系统而言,求解难度会有所下降(比如某个系统内粒子势能与x无关且为定值),但这里我先不做讨论。
但是,我们当初变量分离的时候假定波函数处于定态,如果波函数不处于定态该怎么办呢?
想必很多人都有这样的疑问吧。我告诉你们:当然也适用于非稳态状态下的粒子。还记得我第一次学习推导过程的时候也困惑“这样强令粒子处于定态也太霸道了吧”。
但实际上这一点也不“霸道”,这是基于实验事实提出来的合理设想。我们在文章一开头提到的氢原子光谱就能解释,从氢原子光谱中我们知道“电子所取的能量状态都是预先被自然设定好的”。我们把这种状态称为定态,处于定态的粒子波函数用驻波的波函数表示。
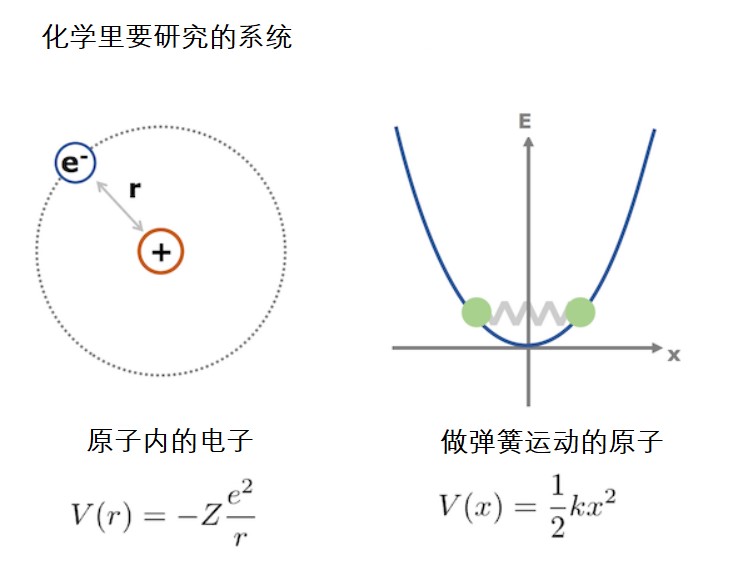
这次的推导过程中还有一个重要的点就是假定势能V只与位置x有关。这是因为在化学讨论的系统内,大多数系统的势能只与位置有关。比方说在原子核周围运动的电子和做弹簧运动的原子群的势能只与位置有关。且不说要是势能还与时间有关,那就没法变量分离了。所以变量分离不是万能的。与时间无关的系统有被光照射的分子。要求与时间无关的系统的波函数需要用到摄动法,这里暂且不作说明。
总结
今天的内容到这里就结束了,我为大家讲解了如何通过设定波函数表示的是驻波从而推导出教科书上面的那个“与时间无关的薛定谔方程”的。在下一篇文章中,我将以最简单的系统——一维深阱作为示例来求解现实里的与时间无关的薛定谔方程。然后,随着系统能量的增加,揭开波函数节点增加的原因以及电子离域使系统稳定的原因。
本文版权属于 Chem-Station化学空间, 欢迎点击按钮分享,未经许可,谢绝转载!



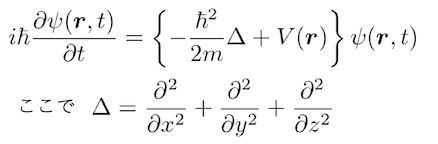


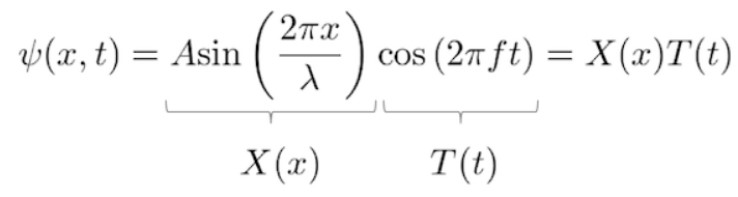



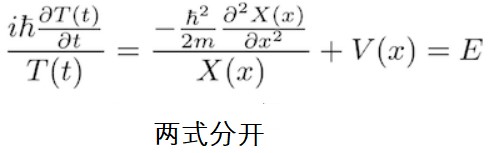


















No comments yet.