本文来自Chem-Station日文版 分子の対称性が高いってどういうこと ?【化学者だって数学するっつーの!: 対称操作】 やぶ
翻译投稿 炸鸡 校对 白菜猪肉馅
我想即使你没有学过群论,你也能大致明白“这个分子的对称性很高”是什么意思。但是如果涉及到要从分子的对称性角度探讨化学问题,知道与对称性相关的专门用语就很有必要了。掌握这些专门用语在借助群论理解分子轨道以及讨论光化学选择律时会发挥很大的作用。今天这篇内容在这篇文章中,我们将讨论对称操作和对称元素,作为学习群论的基础。
分子的对称性高到底是什么意思?
简单的讲,分子的对称性高是指可以对分子执行多种类型的对称操作。下面让我们来详细讲解下。
什么是对称操作?
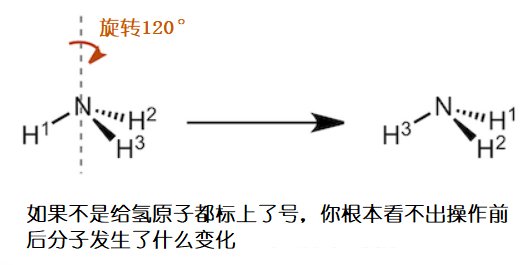
有些物体在旋转或翻转前后,物体的构成要素和方向没有发生变化。比方说你现在背过身去,我偷偷把NH3分子旋转120度,你转过来后能发现NH3分子发生了改变吗?这是因为在操作前后,NH3分子上的各点都移动到了等价的地方。下图中,NH3分子的三个氢原子都标上了1,2,3号,如果没有给它们标号就无法区分旋转过后的它们。像这样如果没有编号就无法区分的物体的排布,称为等价排布。
如上图的操作所示,我们把被操作的物体上面的所有的点移动到了与原来位置等价的位置上的操作称为对称操作。执行对称操作的中心可以是点,线甚至是面,这些统称为对称要素。对称要素也可以理解为执行对称操作时物体上面不动的一部分。因此,当执行“绕某一轴旋转”的对称操作的时候,这个轴上的所有的点都保持不动;当执行“绕某一面反转”的对称操作的时候,这个面上的所有的点都保持不动。
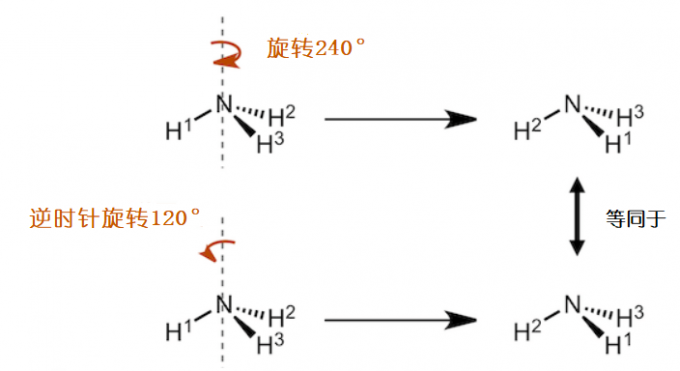
让我们暂且回到文章一开头的那个NH3分子的例子。如果把NH3分子旋转240度,那么分子上的各个点也能回到各自等价的点上。但是如果注意一下氢原子的编号,就会发现旋转240度后的分子排列和旋转120度后的分子排列并不一样。所以旋转240度与旋转120度是不同的对称操作。那么逆时针旋转120度的操作呢? 逆时针旋转120度得到的分子排列与顺时针旋转240度得到的分子排列相同。因此即便给NH3分子上的氢原子编上号,逆时针旋转120度的结果和顺时针旋转240度的结果是一模一样的。故而逆时针旋转120度不能算是新的一种对称操作,只是顺时针旋转240度的另一种表述方式。
顺时针旋转240度和逆时针旋转120度为等价操作
对NH3分子还可以进行除上述操作之外的不同的操作,这一点相信各位读者都很清楚。
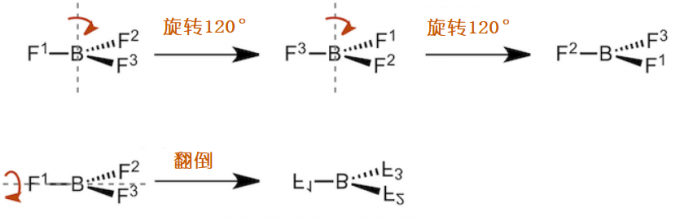
接下来让我们讨论三氟硼BF3分子。和NH3一样,BF3分子逆时针旋转120度和顺时针旋转240度所得到的分子排布是完全一样的。并且BF3分子在一个平面上,所以即使进行翻转操作也能得到等价的分子排布。下图中分子就就被反转了,为了表明有这个翻转过程,元素符号特地上下颠倒了。但实际上原子在翻转前后并没有变化,经过翻转操作后得到了和原来原子排布一样的分子。而NH3是金字塔形的,所以对NH3来说翻转操作不是对称操作。总之,BF3的翻转操作是对称操作,和NH3相比,BF3的对称操作更多,故我们说BF3比NH3的对称性要高。
BF3还有翻转对称操作,所以BF3比NH3的对称性要高。
对称操作是什么?
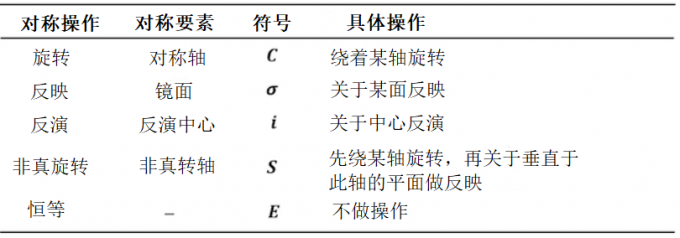
思考分子的对称性的时候,我们只需要考虑5种对称操作或对称要素。下表中大致列出了这5种对称操作或对称要素。因为对称操作和对称元素是一体的,所以它们的符号是一样的。但是请注意,虽然指定了相同的符号,但对称操作和对称元素是不同的术语。对称操作是对分子执行的操作。 而对称元素是指分子中存在的点、线和面。
接下来让我们分别对表中的四个操作和要素一一做说明。
Cn旋转是什么操作?
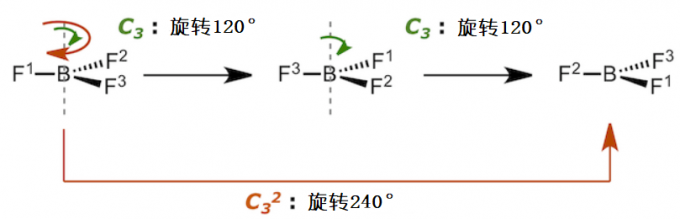
Cn表示旋转360/n度。比如C2 表示旋转360/2=180度;C3表示旋转360/3=120度。
那么旋转240度该怎么表示呢?旋转240度就相当于进行两次旋转120度,仿照数学里的幂写做C32,即表示C3操作重复进行两次。
240度旋转是指进行2次120度的旋转,所以表示为C32。
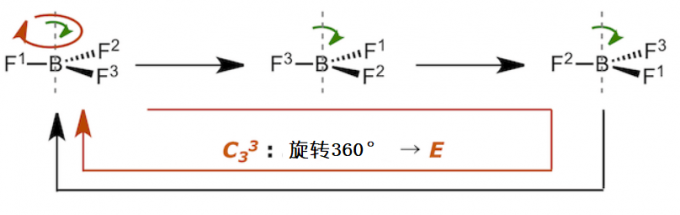
然而,旋转360度并不写做C33 。将分子旋转360度,分子什么变化也没有,等同于不对分子进行操作。不对分子进行任何操作表示为E(恒等操作)。同理,C34所表示的旋转480度就等同于旋转120度。故C34等于C3。
C33表示进行3次旋转120度的操作即旋转360度,所以C33可以表示为E。
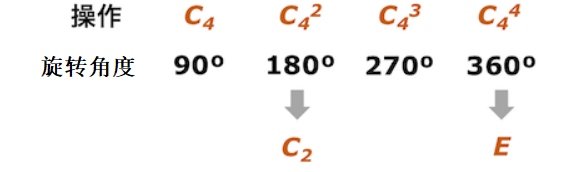
读者们以此类推,C4表示旋转90度。旋转2次90度就等同于旋转180度,所以C42就等于C2,C42可以表示为C2。有些参考书种会写明“C2 (= C42)”,以表示C2 是从C4衍生而来的。C43表示旋转270度,被认为是一类新的对称操作。C44表示旋转360度,用E来表示。
如果绕着某轴进行Cn操作,那么我们把这个轴称为n重转轴(对称轴符号为Cn)。比如我们会说C3操作的对称元素是3重转轴(C3)。但是,C32操作的对称元素却不称为C32。该操作的转轴简称为C3。可以这么理解:转轴的下标数字n对应的是转轴的最高次数。
分子的主轴是什么?
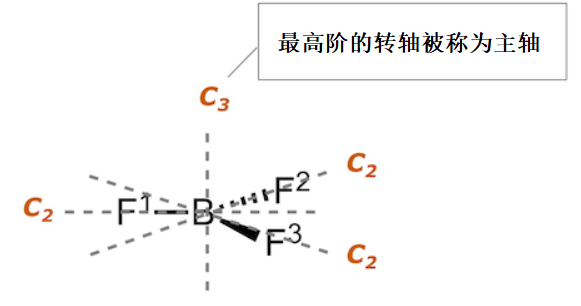
有些对称性高的分子会有多个转轴。遇到这种情况时,我们一般把最高阶的那个转轴定义为这个分子的主轴。下面我们以以下图的BF3为例解释一下。这个分子共有三个转轴,C3转轴分别和两个C2转轴垂直相交。在这3个转轴中,C3转轴为最高阶,故C3转轴为分子的主轴。
反映是什么操作呢?
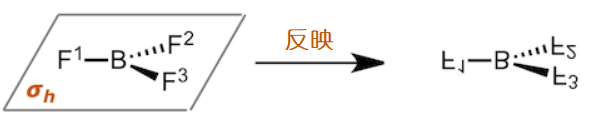
反映是指相对于某个平面(即镜面),把分子翻转的操作。操作符号为σ。比方说BF3分子是平面三角形结构,所以我们可以把BF3分子的平面当成镜面。我们把这样的镜面称为水平镜面,以horizontal的h为下标,表示成σh。
BF3 相对于所在的平面做翻转,分子内部各原子的相对位置没有发生改变。上图为了表示分子已经经历过翻转,所以每个元素符号都 上下颠倒了,但实际上各个原子的排布并没有改变。
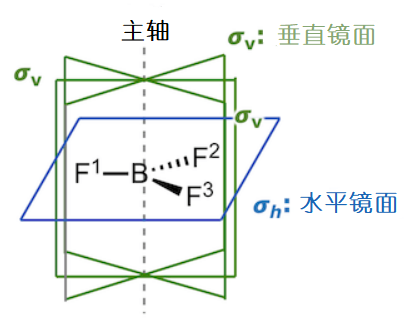
除了水平面,BF3分子还有其他镜面。与分子平面垂直的,包含B–F键的那个镜面我们称之为垂直镜面,用vertical的v作为下标,表示为σv。
严格来说,水平镜面和垂直镜面都是只在分子拥有转轴的前提下才有的定义。换句话说,水平镜面是垂直于分子主轴的镜面,垂直镜面是包含主轴的镜面。但是当一个分子拥有偶数个主轴的情况下,就会存在两种垂直镜面,这时我们把一个垂直镜面称为σv,另一个垂直镜面称为σd。这类情况我们待会详细说明。
σv和σd有什么不同呢?
σd是分子拥有偶数个主轴的时候的垂直镜面,σv和σd所成的二面角是分子主轴旋转角的二分之一。当有两个垂直镜面存在时,哪个面是σv,那个面是σd,是靠惯例决定的。下面我来依次说明。
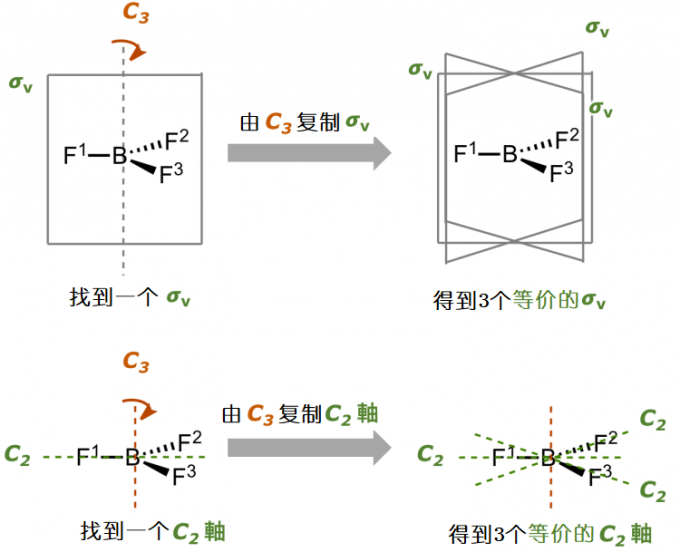
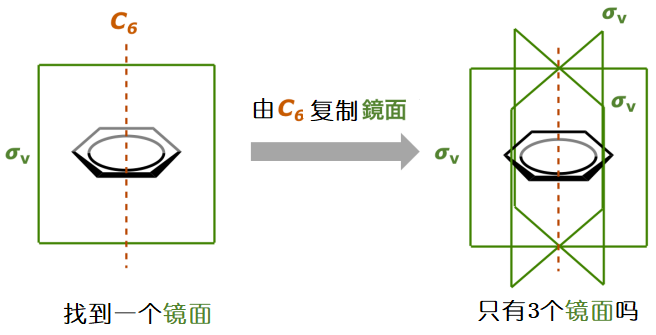
首先要注意的是,主轴的存在可能会复制其它目标元素。比方说BF3,如下图所示它有3个垂直镜面σv。3恰好与分子的主轴 C3的3对应,这意味着只要你找到一个垂直镜面σv,将对应的分子做C3旋转,那么你就会得到一个和这个σv等价的σv,相当于把这个镜面复制了一样,你总共得到了两个一摸一样镜面。同理将对应的分子做C2旋转,同样会得到两个一摸一样镜面。下图中的BF3总共有3个C2 转轴,是经过C2 旋转和C3旋转得来的。
接下来让我们来考虑拥有C6转轴的苯环。苯环的垂直镜面是包含C6轴和苯环六角形对角线的面。这些垂直镜面也是经过C6旋转得来的。这样说的话难道和其中一个镜面等价的镜面有6个吗?不是的,正确答案是只有3个。为什么呢?因为进行3次C6旋转后就相当于旋转了180度,旋转180度,分子就回到了原来的位置。
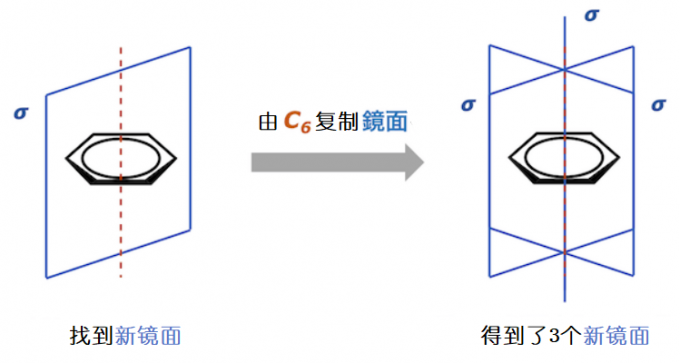
但并不是说苯环的只有3个镜面。切割C-C键的面也算是镜面。该镜面平分苯环对角线形成的夹角。这类镜面经过C6旋转复制后变成了3个。
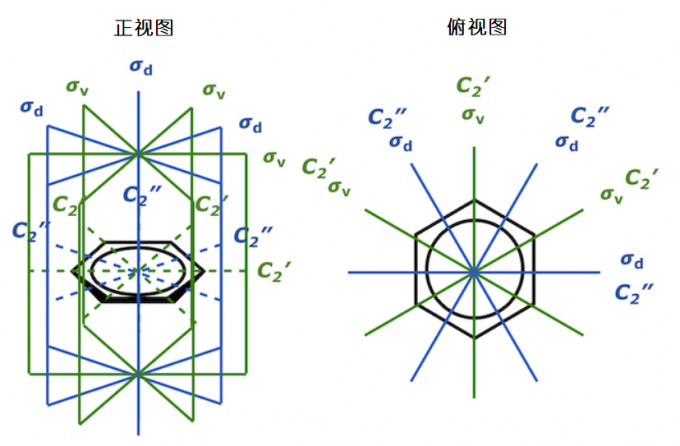
综上所述,苯环共有两种镜面,每种镜面各3个,共计6个垂直镜面。个数正好与苯环的转轴C6的6一致。但是,与BF3时不同,与苯环垂直的6个镜面之间并不相互等价。按照惯例,包含六边形对角线(C2’轴)的面被正式命名为垂直镜面σv,作为真正的垂直镜面。而切割C-C键(C2” 轴) 的垂直镜面因为和C-C键形成了二面角的关系,取dihedral的的为下标,命名为σd。σv和σd所成的二面角恰好是主轴旋转角的二分之一。
从C2转轴出发也可以得到同样的结论。苯环有与主轴垂直的C2轴,共有6个,但是这6个C2轴并不相互等价。形成六边形对角线的C2转轴被命名为C2’,而将C2’分成两部分的C2转轴(即连接彼此面对面的C-C键的中点的线)被命名为C2”。
请读者们一定要谨记,只有当n为偶数的时候σd才存在。BF3的主轴是C3,3为奇数,所以对于BF3而言,它所有的垂直镜面都是等价的,所以BF3所有的垂直镜面都命名为σv。
如果有垂直于主轴Cn的C2轴或垂直镜面,则可以通过主轴旋转操作复制这些轴。 此时:
如果n是奇数,那么n个C2转轴和垂直镜面σv都是等价的。
如果n是偶数,则存在两类C2转轴或垂直镜面σv,每类各有n/2个。
反演是什么操作?
将分子中的每个原子通过分子中心的一个点投射到该点另一侧的操作称之为反演,通过的分子中心的那个点称之为反演中心。操作符号为i。
恒等是什么操作?
恒等操作就是不对分子做任何改变的操作。符号为E。恒等操作没有对称元素。
非真旋转是什么操作?
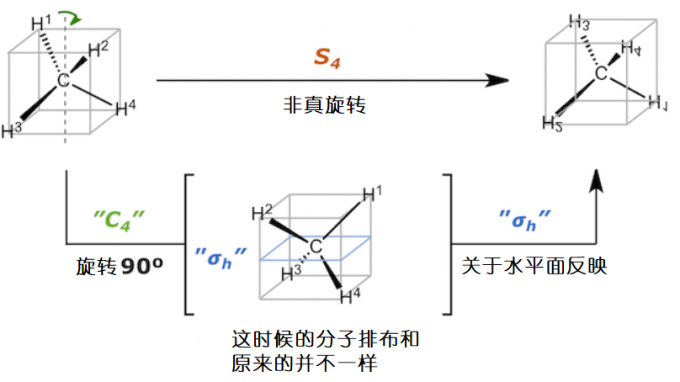
非真旋转是指将物体绕某轴旋转一定角度后,然后对垂直于该转轴的平面进行反映的操作。当然你也可以先反映再旋转。非真旋转英译为 improper rotation或rotary reflection,符号为Sn。S是来自德语里“镜子”一词spiegel的首字母。我们拿甲烷CH4来具体展示下非真旋转是什么把!以平分H-C-H键的轴为转轴,旋转90°,然后再反映,得到了和原分子一样的分子。所以甲烷存在一个S4的对称操作。
但并不是说一个分子有Sn对称操纵,这个分子就一定有Cn操作。从上图的甲烷的例子中我们可以看到,原来的甲烷分子旋转90度后,并没有得到和原分子一样的分子。氢原子的排布发生了改变。因此甲烷的S4转轴并不是C4转轴。因此,在上图中S4中间的90度旋转被标记为”C4”。旋转之后的反映操作也是同理,并不是甲烷真正的反映操作。
也有一些非真旋转操作和其他对称操作等价。比如S1操作,先做C1旋转然后做关于与C1转轴垂直的平面的反映。但是C1操作是将分子旋转360度,可以说等于没有对分子进行操作。所以S1操作等价于单纯的反映操作。同样的,S2操作是先将分子旋转180度然后反映,就相当于对分子做一个反演操作i。
为什么要把非真旋转单独当成一种操作呢?
有些读者可能会疑惑:非真旋转无非是先旋转再反映,明明是一类复合操作,为什么要单独被命名为一种操作呢?但是,实际上非真旋转操作是一类明显的对称操作,必须被认可。原因有两个:一是如果没有非真旋转操作,单单一次操作是无法再现甲烷的所有等价排布的。
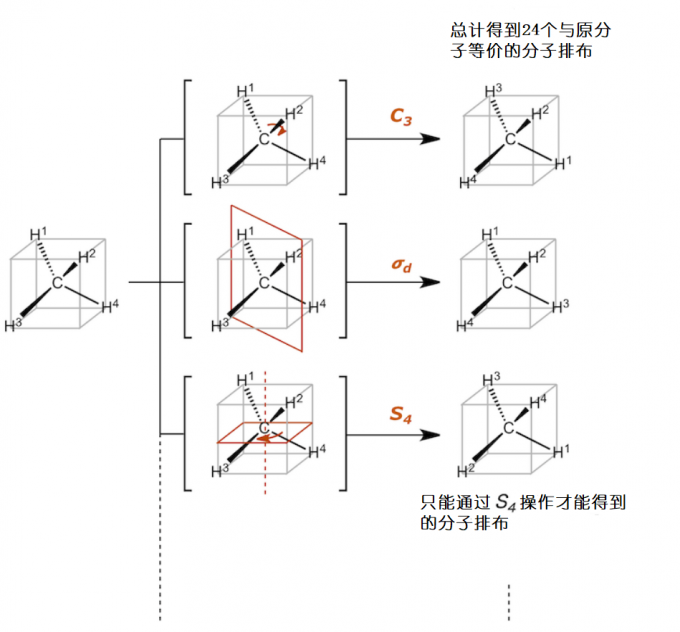
我们来举个例子说明下吧。读者请看下图,甲烷分子是个四面体结构,我把四个顶点都依次标上了号。那么计算下来共有4 x 3 x 2 x 1 = 24种排布。我在文章的前半部分说:“把一个物体的所有点移动到等价点的操作叫做对称操作。”反过来说,从一个位置移动到等效位置的所有操作都被认为是对称操作。比如下图右列最上方的那个排布是左列最上方的那个排布经过C3旋转得到的。右列第二行的排布是经过反映操作得到的。那么第三行的排布又是怎么得到的呢?是通过非真旋转操作S4得到的。如果不允许非真旋转操作作为一类单独的对称操作,甲烷的24种等价配置就无法对应。
CH4的排布存在24种可能性,如果不把S4看作独立的一类对称操作的话,就不能在一次操作中得到全部的甲烷分子排布。
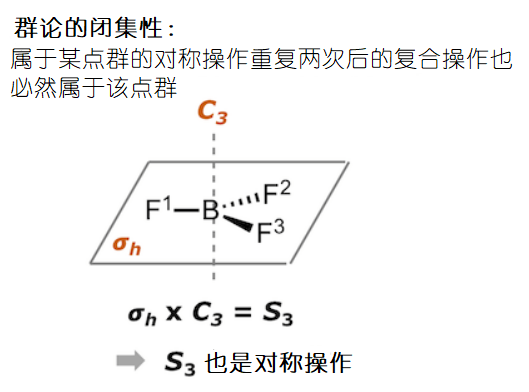
把非真旋转操作当成一类独立的对称操作的第二个原因是群论的闭集性。群论的性质我会在之后的文章里再详细介绍,现在读者们只要明白属于某点群的对称操作重复两次后的复合操作也必然属于该点群。比如BF3分子属于D3h 点群,同时拥有3重转轴(C3)和σh 镜面。因为群论的闭集性,C3和σh 组成的复合操作也同样属于D3h的对称操作。C3和σh 组成的复合操作就是S3。所以非真旋转操作S3也必然属于D3h点群的对称操作。
重复进行非真旋转操作会发生什么事?
同Cn操作一样,重复进行Sn操作也用平方表示。n为奇数时和n为偶数时的情况不一样。
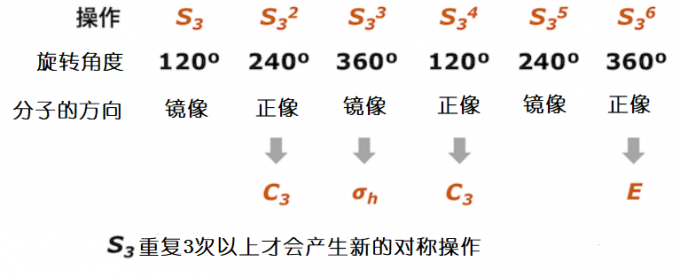
比如S32表示先把分子旋转120度然后反映,又旋转120度再反映。但是因为进行了两次反映操作而且还都是针对同一面(反映的镜面是与分子主轴垂直的面,两次反映的面是同一个面),所以S32就相当于旋转240度。S32=C32。那么S33呢?我们可以这么想:S33就是进行3次S3操作,我们刚刚已经知道S32等于旋转240度,那么我们只要在把分子旋转240度的基础上再旋转120度,反映。故分子总共旋转360度,又因为分子总共进行了3次反映,进行两次反映就相当于不做反映,所以进行三次反映我们可以认为是进行了一次反映。所以S33等价于反映(= σh)。
续进行3次S3操作没法让分子回到原来的状态。那么进行4次S3操作呢?S34等于先进行S33,再进行S3,我们已经知道S33 等价于反映,那么S34就是先对分子做反映操作,再旋转120度,反映。分子共计进行了2次反映,2次等价于没有反映所以分子只做了旋转120度操作,故而S34等于C3。但情况到了S35这里又有点不一样,S35是在S34基础上再进行一次S3,相当于把分子旋转240度(120*2)然后再反映,是个新操作。所以S35只能表示为S35,并不能用其他操作符号表示。S36就相当于把分子旋转240+120=360度,进行两次反映相当于没有进行反映,所以S36等价于恒等操作E。到进行到S36这里,分子才相当于做了一个恒等操作,S3到S36可以说是一个轮回,分子又回到了原来的那个分子。到了S37以后分子也就没有新操作了,因为S37以后的操作都等价于S3-S36中的一个操作。综上所述,通过重复S3操作,可以获得六个操作:S3,C32,σh,C3,S35和E。
Cn操作和S3操作同理,因为当分子累积旋转360度后就相当于相当于做了个恒等操作,所以就没必要考虑Cnn+1以上的对称操作了。但也有的非真旋转操作Sn,即使重复n次也不会返回到原始的分子排布。
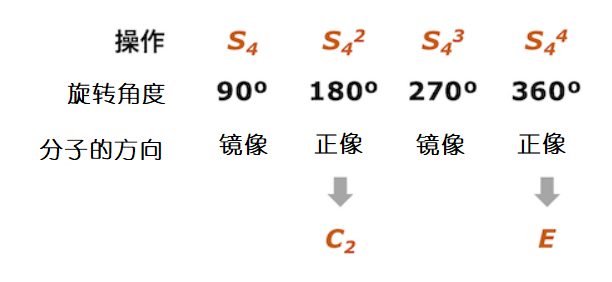
那如果n为偶数呢?我们那S4做个例子吧!S42相当于旋转180度,为C2。S44相当于把分子旋转360度,为恒等操作。S4-S44是一个轮回,S44往后的操作都不算是新操作了。
以上我们讨论了n为奇数时,重复Sn会发生什么和n为偶数时,重复Sn会发生什么,我们可以总结出这样一条规律,当n为奇数时,重复n次Sn操作(即Snn)等价于对分子进行反映操作,所以具有Sn(n为奇数)对称操作的分子必然有σh 操作。所以进行n次以上的Sn操作也算作新操作。但若n为偶数,重复n次Sn操作,就相当于对分子做了个恒等操作。因此当n为偶数时,Snn=E,进行n次以上的Sn操作并不算作新操作。这一规律对于了解Sn操作的循环很有用。
n为奇数时,Snn=σh
n为偶数时,Snn=E
结束语
本文讨论了对称操作和对称元素的术语。许多无机化学教科书书和物理化学教科书上也有这块内容的介绍,但是我今天这篇文章讲的要比教科书上细致很多。
不过,很多人在学习了对称操作之后,都有过这样的想法:
“这个对称操作和群论有什么关系? 到底什么是群论?”
针对这个疑惑,在下一篇文章中,我将讨论什么是群,看看分子对称操作是怎么形成群的。在下一篇文章的最后,我会揭开教科书最后一页的指标表是怎么来的。
相关记事
为什么电子要离域或定域?【带你再次走进薛定谔方程:一维深阱式势能和曲率】
参考文献
- Cotton, F. A. Chemical Applications of Group Theory, 3rd edition, 1989, Wiley.
- 原田義也 量子化学 下巻, 2007, 裳華房.
























No comments yet.