电子由低能级跃迁到高能级需要满足自旋不变、轨道对称的条件、轨道重叠以及包括光矢量与跃迁矩作用方向决定了跃迁概率。那么退激的过程需要满足哪些条件以及会产生什么现象呢?
Q1:首先能量转移有哪几类?
A1:能量转移是指处于高能级的电子的能量传递过程,主要分为分子内和分子间的能量转移过程。以下分别详细介绍:
分子内的能量转移
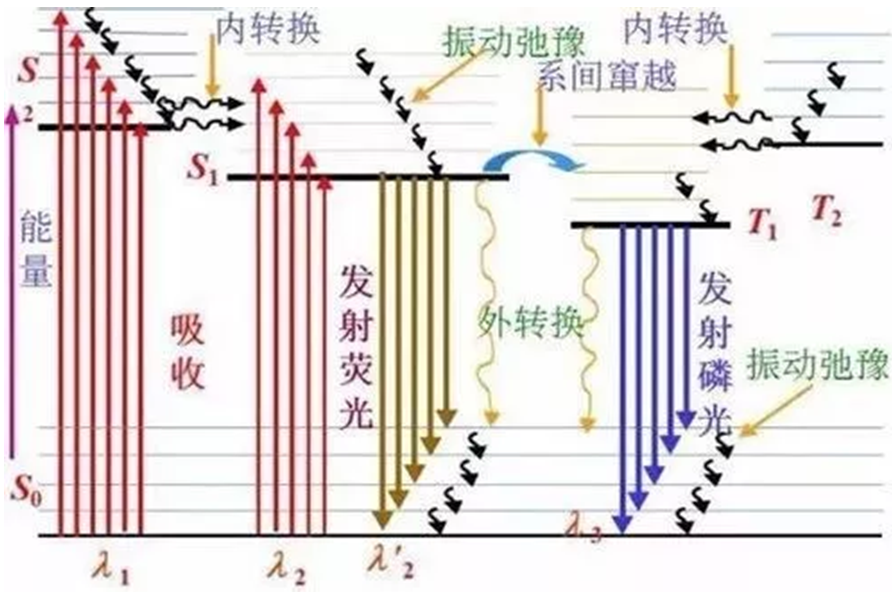
分子内的能量转移过程可以有Jablonski图展现出来,包含内转化、振动弛豫和系间窜越三类。振动弛豫过程使激发态的电子—通过和其它的分子振动能级耦合—能够释放出激发态上高振动能级的能量,最终实现了分子激发态非辐射衰变过程。
分子内能量转移Jablonski图
分子内的能量传递过程涉及到两种状态—高能与低能,偶极矩变化等—随时间的变化,在描述这种过程的跃迁速率常数时,都可以选择用Fermi黄金规则来描述:![]()
算符H为驱动跃迁这一过程的哈密顿算符,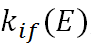 为分子内的传能速率,由上式可知,其与两种状态的轨道的重叠耦合作用的平方以及态密度
为分子内的传能速率,由上式可知,其与两种状态的轨道的重叠耦合作用的平方以及态密度![]() 成正比。这两个物理量的理解可以认为:
成正比。这两个物理量的理解可以认为: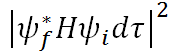 是两原子轨道重叠积分的概率密度,几何意义代表的是两个轨道间重叠程度的平方。重叠越多,跃迁的能垒越低。而态密度
是两原子轨道重叠积分的概率密度,几何意义代表的是两个轨道间重叠程度的平方。重叠越多,跃迁的能垒越低。而态密度![]() 则表示单位频率内振动能级数也可以理解为振动能级密集性,因而直观上理解:振动能级越密集,振动能级间的重叠程度越高,内转化过程能垒越低,因而越容易实现传能。
则表示单位频率内振动能级数也可以理解为振动能级密集性,因而直观上理解:振动能级越密集,振动能级间的重叠程度越高,内转化过程能垒越低,因而越容易实现传能。
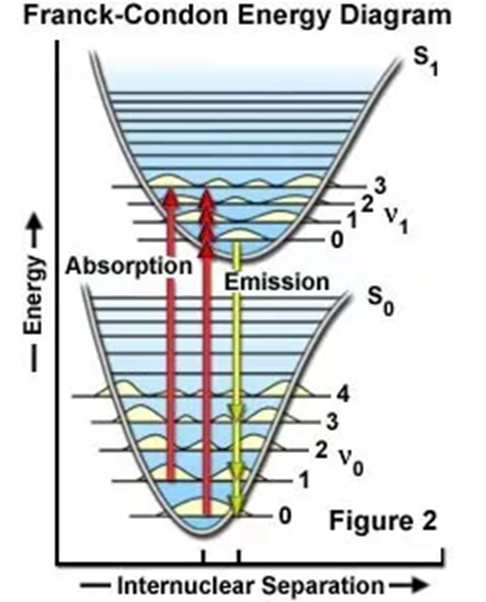
Franck-Condon轨道重叠
吸收光谱由振动选择规则以及Franck-Condon重叠决定—前面有具体介绍,而发射光谱则在上面图中的![]() 处发生,振动弛豫传递走了过多的振动能级能量。因此内转化是
处发生,振动弛豫传递走了过多的振动能级能量。因此内转化是![]() 与
与![]() 某处振动能级间的重叠处开始的。
某处振动能级间的重叠处开始的。
Q2:微观体系中的能级跃迁多借助于能级间的重叠,那么良好的能级重叠取决于哪些因素呢?
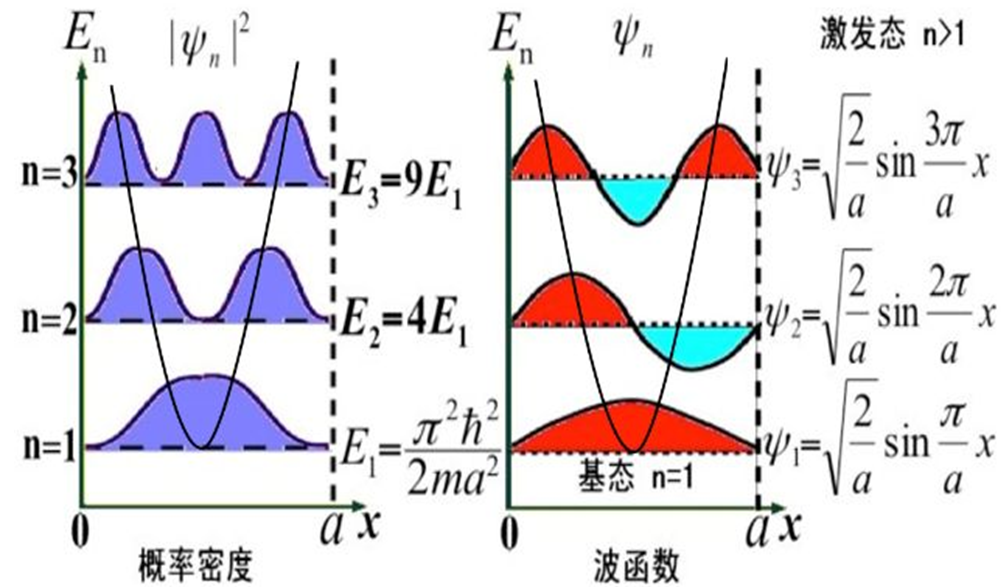
A2:不同激发分子振动跃迁重叠程度的大小与化合物分子基态和激发态势能曲线形状以及能隙大小等因素相关。下图是一维势阱中的波函数形状。
不同能级的波函数在一维势阱中的驻波及其概率密度
当基态与激发态有着相似的几何形状以及较大的能隙时,往往是不良重叠;而能隙较小以及几何形状相近的,或者能隙较大但是几何形状不同的,则往往具有良好的重叠。跃迁可以看做是发生在HOMO与LUMO轨道上—最可几,其能隙大小影响了光谱分布,以及能量转移速率。随着能隙增大,分子内能量转移速率降低。一般情况下,态-态间能隙大小为:![]() .因而
.因而![]() 的非辐射传能速率最慢,这个关系似的意义在于:可以通过改变分子结构,可以实现系间窜越速率大于内转化速率。如下图所示,随着系间窜越能垒越来越高,系间窜越速率也在逐渐降低。但是值得注意的是这和共轭体系大小的关系吻合得不是很好,因而也反映上面提出的几何构型对能量转移速率的影响。
的非辐射传能速率最慢,这个关系似的意义在于:可以通过改变分子结构,可以实现系间窜越速率大于内转化速率。如下图所示,随着系间窜越能垒越来越高,系间窜越速率也在逐渐降低。但是值得注意的是这和共轭体系大小的关系吻合得不是很好,因而也反映上面提出的几何构型对能量转移速率的影响。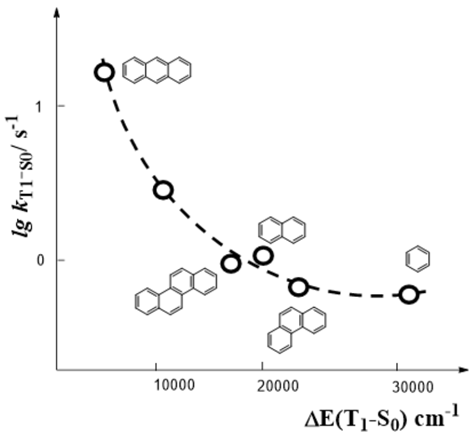
荧光分子的跃迁速率与能极差间的关系
分子间的能量转移
分子间的能量转移分为两种:辐射能量转移和非辐射能量转移两种,总的关系式可以用以下的关系式表示:
其中Donor, Acceptor分别表示能量给体和能量受体。*表示激发态。
分子间的辐射能量转移机制由于涉及到辐射出光子的过程,因而可以用以下的过程简单描述: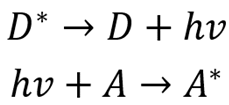
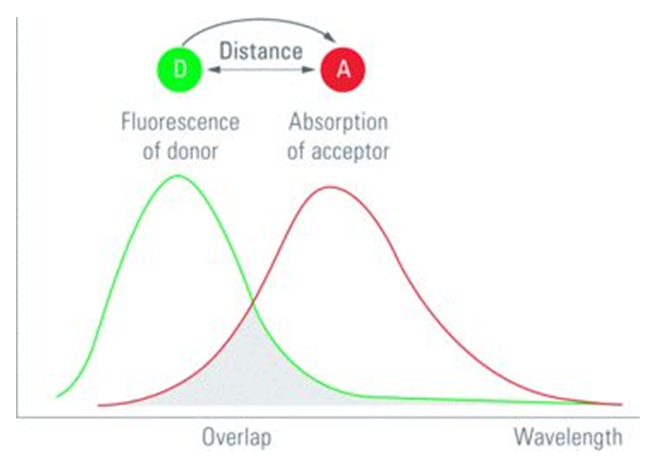
这就涉及到一个中间的过程为:D发出了光,光子接下来被A内吸收,并实现了激发。因而其带来的特征是只要符合A的辐射激发规则就能够实现体系中长程激发:长距离的能量传递。A的吸收光谱和D的发射光谱重叠积分越大,其能量转化效率越大。
辐射能量转移容易理解之处在于其过程实质上是前面讲过的激发的跃迁选律和分子内非辐射能量转移过程的一个分子间耦合过程。
Q3:那么分子间的能量转移除了辐射能量转移机制外,其它的诸如非辐射能量转移机制有哪几种方式?
A3:概括起来包括三种:Foster能量转移、Dexter电子交换能量转移机制以及载流子陷阱捕获机制的能量转移机制。以下主要介绍Foster能量转移机制
非辐射共振能量转移
Foster能量转移机制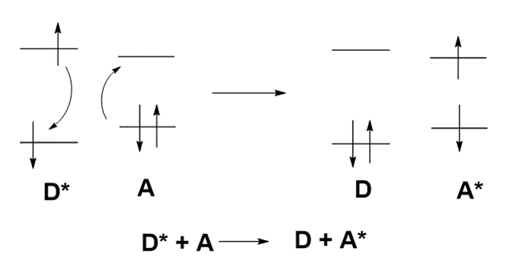
Foster能量转移机制
Foster能量转移机制是通过激发态D*与基态A之间的共振而引起的能量转移。这个过程涉及的是态-态之间的跃迁,因而跃迁也需要跃迁的选择规则:相同的多重态之间发生。同样的原理,在波恩-奥本海默近似下,跃迁过程可以看做是微扰的态-态变化过程,同样符合Dirac的Fermi黄金规则,用以下公式表示: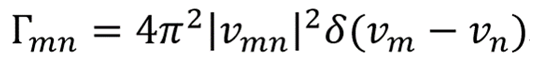
![]() 表示从能量给体态m跃迁到受体n的能量转移速率,
表示从能量给体态m跃迁到受体n的能量转移速率,![]() 表示态-态间的相互作用矢量的乘积值—轨道的作用是矢量的,也可以描述成是轨道重叠程度。公式中最后面两者则分别是给体态的能量和受体态的能量。正是在微扰理论的前提下,Fermi黄金规则里面的哈密顿算符H可以分解为
表示态-态间的相互作用矢量的乘积值—轨道的作用是矢量的,也可以描述成是轨道重叠程度。公式中最后面两者则分别是给体态的能量和受体态的能量。正是在微扰理论的前提下,Fermi黄金规则里面的哈密顿算符H可以分解为![]() ,带时间项和不带时间项,因此H可以看做是含时间的算符。这就导致发生微扰后的体系在能量守恒的条件下:存在角频率的振荡,从而不同态之间的能量是不一样的—解释了跃迁的能级间的能量关系,根据跃迁选律,只有能量相同的态之间,才能发生共振耦合,因而才会有跃迁发生,从而
,带时间项和不带时间项,因此H可以看做是含时间的算符。这就导致发生微扰后的体系在能量守恒的条件下:存在角频率的振荡,从而不同态之间的能量是不一样的—解释了跃迁的能级间的能量关系,根据跃迁选律,只有能量相同的态之间,才能发生共振耦合,因而才会有跃迁发生,从而![]() 不为0。用函数表示这个限制时,可以引入δ函数—δ函数表示
不为0。用函数表示这个限制时,可以引入δ函数—δ函数表示![]() 时,函数值为1即允许的过程,否则为0即禁阻的过程。
时,函数值为1即允许的过程,否则为0即禁阻的过程。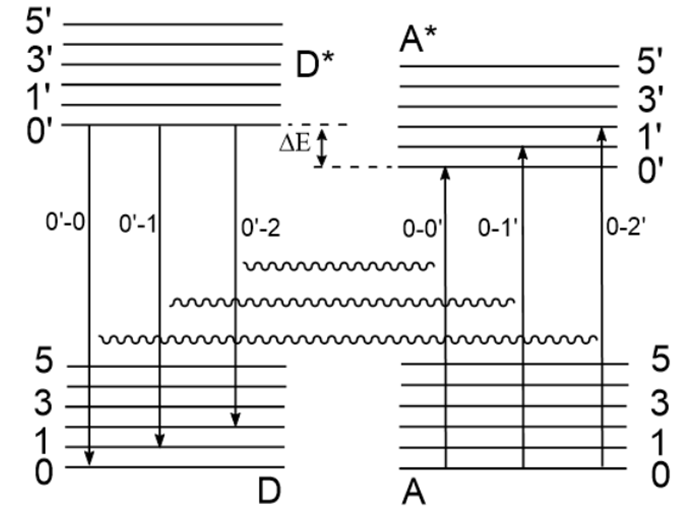
Foster能量转移机制
上面的图显示的是Foster能量转移过程的给体和受体间的相互作用。左侧现实的是给体在激发态的基态振动能级间发生退激,跃迁矩大小为![]() ,为Franck-Condon重叠,
,为Franck-Condon重叠,![]() 为电子跃迁矩。同理,受体激发的跃迁矩为
为电子跃迁矩。同理,受体激发的跃迁矩为![]() 。两者相等时发生共振能量转移。数学推导出共振能量转移过程中,总的给体和受体间的转移速率公式:
。两者相等时发生共振能量转移。数学推导出共振能量转移过程中,总的给体和受体间的转移速率公式: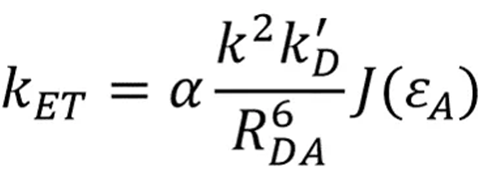
α是受浓度—自吸收以及碰撞会产生影响和溶剂折射律—前者是相对磁导率,后者是为相对介电常数—影响的常数,![]() 是空间内受偶极取向影响的两振荡偶极间的相互作用。一般无规分布的偶极间的相互作用时,k都取常数2/3,最后面的是重叠积分项—依旧是轨道重叠,J是关于吸光系数
是空间内受偶极取向影响的两振荡偶极间的相互作用。一般无规分布的偶极间的相互作用时,k都取常数2/3,最后面的是重叠积分项—依旧是轨道重叠,J是关于吸光系数![]() 的函数。
的函数。![]() 是两偶极间的距离的6次方,由6次方可知是一种短距离作用。由上面的函数关系式即可知道Foster共振能量转移方式速率的提高应满足:
是两偶极间的距离的6次方,由6次方可知是一种短距离作用。由上面的函数关系式即可知道Foster共振能量转移方式速率的提高应满足:
光谱重叠积分与能量转移效率
- 给体的辐射速率常数
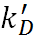 越大,则能量传递过程能迅速进行。且受到分子间的碰撞淬灭的概率越低,因而有利于提高能量的转化效率
越大,则能量传递过程能迅速进行。且受到分子间的碰撞淬灭的概率越低,因而有利于提高能量的转化效率 - 两相互作用的偶极间的距离越短,其传递能量的速率迅速增加。当然的距离
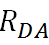 不可能是0,靠得太近会受到静电排斥作用,这种大小也是与距离的6次方成反比。因而俩偶极间的距离会存在一个临界距离
不可能是0,靠得太近会受到静电排斥作用,这种大小也是与距离的6次方成反比。因而俩偶极间的距离会存在一个临界距离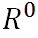 ,一般在10nm以内。加上临界距离的影响的话,则:
,一般在10nm以内。加上临界距离的影响的话,则: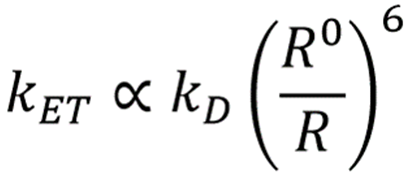
因此减小临界距离也是能够提高能量转移速率以及效率的高效方法。除了这种方式外,还有采用链接的方式实现FRET荧光共振能量转移从而起到光分析等目的。以下的方式较为常见: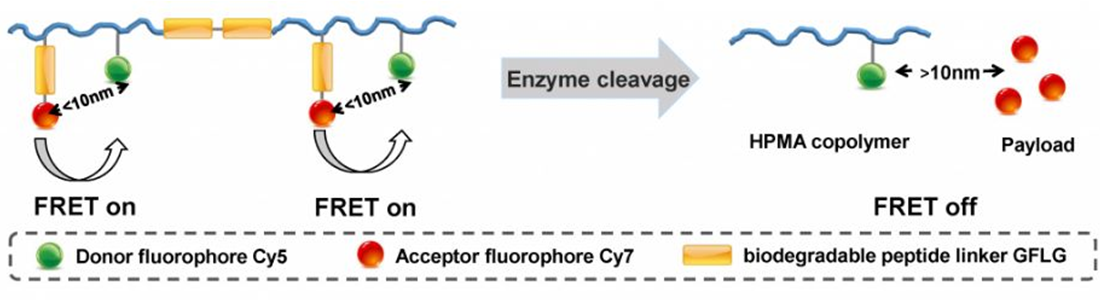
用FRET过程设计丰富的探针
- 对于
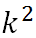 项则需要有较好的偶极取向,角度间的依赖关系符合:无规取向时k=2/3,头尾取向时k=-2,平行取向时k=1。
项则需要有较好的偶极取向,角度间的依赖关系符合:无规取向时k=2/3,头尾取向时k=-2,平行取向时k=1。
总结:
讲解了分子内和分子间的能量转移机制,以及辅助理解的Fermi黄金规则和能够指导实验的能量转移速率公式
思考:
1:增加荧光发射为什么需要刚性结构?—振动能级
2:Fermi黄金规则可以解释的很多化学物理现象—以NMR为例,在强磁场作用下能级发生裂分,在提供射频波辐射时,是否需要担心:原子核振动能级也会发生跃迁和退激,从而发射出能量从而干扰核磁谱信号呢?答案是否定的:依据Fermi黄金规则自发辐射的速率正比与光子的态密度,光子的态密度与其频率的平方成正比。实际上,原子自发辐射的速率与其放出光子的频率的三次方成正比,指数中2次方来自态密度,1次方来自耦合强度。所以,微波频段的自发辐射速率比可见光波段的自发辐射慢了至少10个数量级,这种差异是可以采用脉冲激发消除背景的。
3:用费米黄金规则解释天空为什么是蓝色的?—瑞利散射强度与频率四次方成正比,蓝光频率是红光的1.8倍,散射强度比红光大接近10倍
4:如何通过调节分子结构的方式来增加能量转移效率?以上四个因素的分子改造因采取什么思路?—极性,次级键等
本文版权属于 Chem-Station化学空间, 欢迎点击按钮分享,未经许可,谢绝转载!

























No comments yet.