译自Chem-Station网站日本版 原文链接：群ってなに？【化学者だって数学するっつーの!】

翻译：炸鸡

在上一回《分子的对称性高到底是什么意思？【化学家也要学数学吗！：对称操作】》中我们学习了分子的各种对称操作和归属的点群。今天，我们来学习一般教科书中很少提及的“点群”。彻底理解了点群，也就明白了无机化学和物理化学教材末尾那张难懂的指标表了。本文还配有简洁易懂的关于群论术语的解释，所以请读者不要担心内容深奥难以理解。好啦！让我们上车！

读前须知

想必大学三四年级的学生和研究生都听过“分子的对称性”和“群论”这两个概念。判断分子对称性并归属点群是应试的基本技能之一吧。考完试很少有同学去刨根问底“那么，什么是群论呢”。这也有本科教科书的锅，因为很少有本科的化学教材会认真向学生科普什么是群。只有少数高阶的物理化学和有机化学教材会写有根据群论推导出的对称性线性组合（Symmetry Adapted Linear Combinations，SALC）的过程。在没有扎实打牢群论的基础上就贸然进入群论的应用是件挺让人担心的事。

本文将解答“什么是群论呢”，还会详解群的定义和相关术语。但把话说在前头：本文将要讲的知识不是化学的实际应用的必备知识（这是很多化学教材忽略这一部分的原因），而且如果你是准备考试的学生，这篇文章可能对你的考试起不到直接的作用。但是扎实的基础知识能帮助你照亮实际应用上的一些小盲区。如果你想在化学里游刃有余地使用群论但又看不懂数学教材上的群论的话，这篇文章会让你豁然开朗。

群是什么

群是满足下列以元素之间的“积”定义的条件的元素的集合。

性质1：一个元素和另一个元素的“积”也必定是这个集合的元素（闭集性）

性质2：当考虑三个或多个元素的“积”时，计算的顺序并不影响结果。（结合性）

性质3：集合内总存在一个元素，这个元素与集合内其他元素的“积”就是这个元素本身（存在单位元）

性质4：总存在一个元素，它与另一个元素的“积”为单位元。（存在逆元）

稍稍说明下。这里的 “积 ”不一定都是乘法的结果。加法的结果在一些情况下可以被定义为一个群的 “积”。一言蔽之，任何计算和操作的结果都可以被称为“积”。等看到后面你就会明白这些元素甚至不一定是数字，“积”不仅仅指数字结果。

群长什么样

为了让读者彻底理解上面所说的群的性质，我们来看看一些具体的群吧。

例1.将“积”定义为加法的结果，全部的实数集合是一个群吗？

这满不满足群的定义呢？首先思考满不满足闭集性。实数相加一定是实数，所以性质1 的闭集性满足。其次，思考满不满足结合律，加法本身就满足结合律，所以性质2也满足（(1+2)+3 = 1+(2+3)）。再考虑满不满足存在单位元的要求。一个实数与另一个实数相加，另一个实数不会改变，有这样的实数吗？有，那就是0。0就是单位元。所以性质3也满足。那么最后有没有满足性质4呢？存在一个实数，当它与其他实数相加结果等于0吗？当然有，1+（-1）=0。对于实数x，-x就是逆元。

所以，如果“积”被定义为加法的结果，所有的实数组成的集合是一个群。

例2.将“积”定义为乘法的结果，全部的实数集合是一个群吗？
让我们来思考满不满足群的四个性质。性质1和性质2自不必说，都符合（因为都是实数的乘法）。性质3满不满足呢？数字1就是一个单位元，1与任何实数相乘就等于原来的实数。逆元存在吗？存不存在与一个实数相乘结果为1 的实数呢？5*(1/5)=1，但我们能说对于实数x，逆元就是1/x吗？不能这么说！因为如果对于0，我们不能说0的逆元是1/0。所以积被定义为乘法的结果时，实数集合不满足群的条件的。但是，在将‘积’定义为乘法的结果时，除0外的所有实数组成的集合是群。

例3.将“积”定义为乘法的结果， 集合{1, –1, i, –i}是一个群吗？

i表示虚数。先看看满不满足结合律和单位元。如果“积”定义为乘积，自然满足结合性。1自然是单位元。

满足了两个性质后，再来思考闭集性。这需要计算出所有元素的乘积，有点麻烦了。为了方便起见，我做个积表（multiplication table）（下图），表的第一行和第一列都是元素，从这个表格我们可以清楚看到每个元素互乘的结果。计算过程被省略。

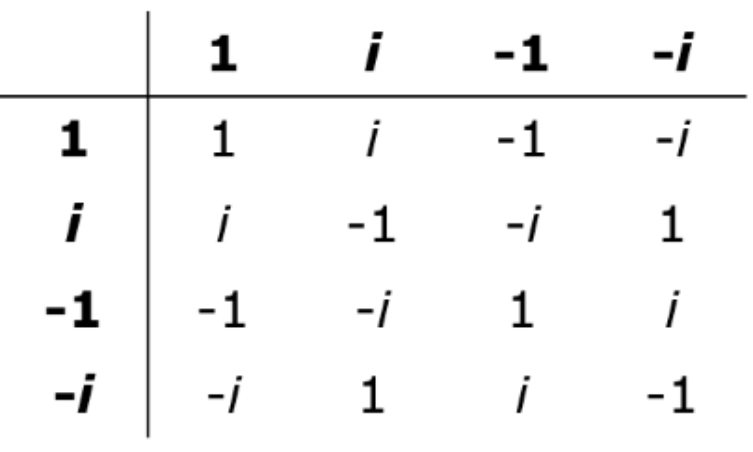
Imaginary group, I = {1, i, -1, -i} 的积表，每个元素的乘积会汇总

表中显示的乘积只有{1, –1, i, –i}。就这满足了闭集性的要求。仔细观察表就会发现所有的行或是列里一定有数字1。比方说i所在的第二行，（-i）*i=1。所以i的逆元是-i。如此看来，所有的元素都存在对应的逆元。将“积”定义为乘积时， {1, –1, i, –i}是一个群。这个群被称为imaginary group ，符号为I。

例4.将“积”定义为连续操作的结果，物体（分子）的对称操作的集合是一个群吗？

这里就稍微有一点变化了，群的元素不再是数字了，群的元素变为了对称操作。“积”被定义为“连续实施2个操作的结果”。让我们从简单的分子-氨开始考虑（对对称操作不熟悉的读者可以参看：分子对称性高是什么意思）对氨分子来说，存在以下6个对称操作。

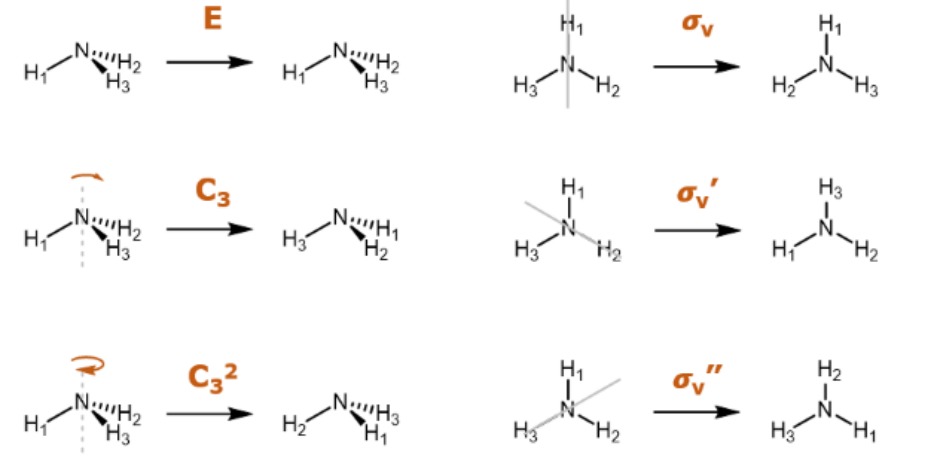
氨分子的6个对称操作E, C₃, C₃₂, σ, σ’, σ”

这6个对称操作中任意两个叠加会产生什么效果呢，让我们做个积表吧。因为操作的先后不同“积”也不同，所以这里规定先进行行的操作再进行列的操作。

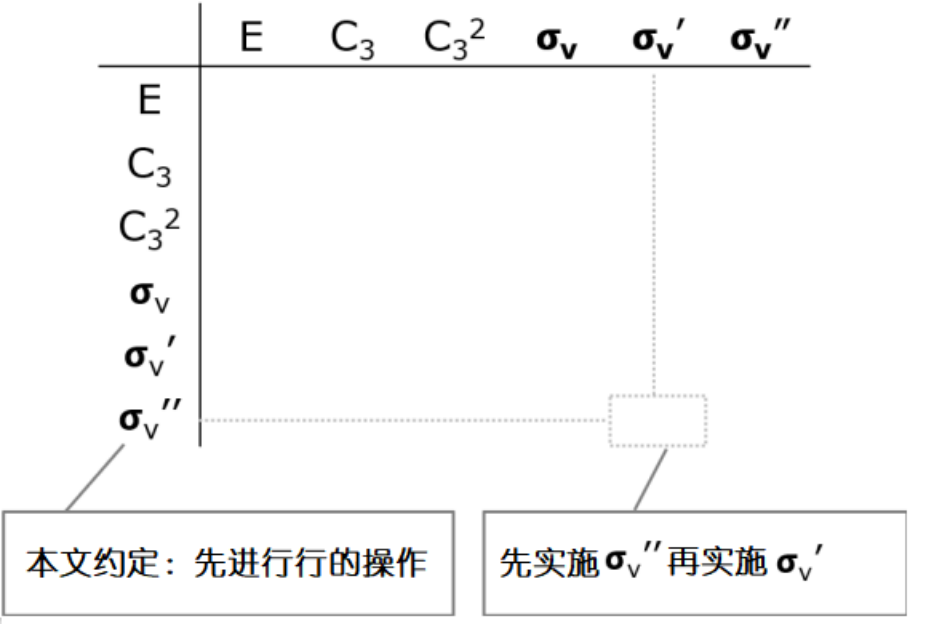
对称操作的积表的规定。元素的先后顺序对称操作的积有影响，规定先进行行的操作。

说完了规定，让我们正式开始填充积表。首先是E列。E的行和列很容易填写，因为无论你把E乘以什么，结果都不会改变。接下来，考虑 “C₃*C₃“，因为C₃是一个120°的旋转。连续做两次相当于做一次240°的旋转，即C₃₂。“C₃*C₃₂”，意为先旋转120°再旋转240°，相当于不做任何改变地旋转360°，即是恒等操作E。

填充完了E行和一半C₃行的积表。接下来考虑“C₃*σv”

“C₃*σv”会有什么结果呢？稍微有点难懂。要是有立体投影图（stereographic projection）就容易想象了。想象我们俯视氨分子，取氨分子上的某一点，这个点经过第一个对称操作后移动到了一个位置， 后经过第二个对称操作后点又再次移动到另一个位置。我们可以把两个对称操作的积简化为把这个点从起始位置直接挪到最终位置的操作。

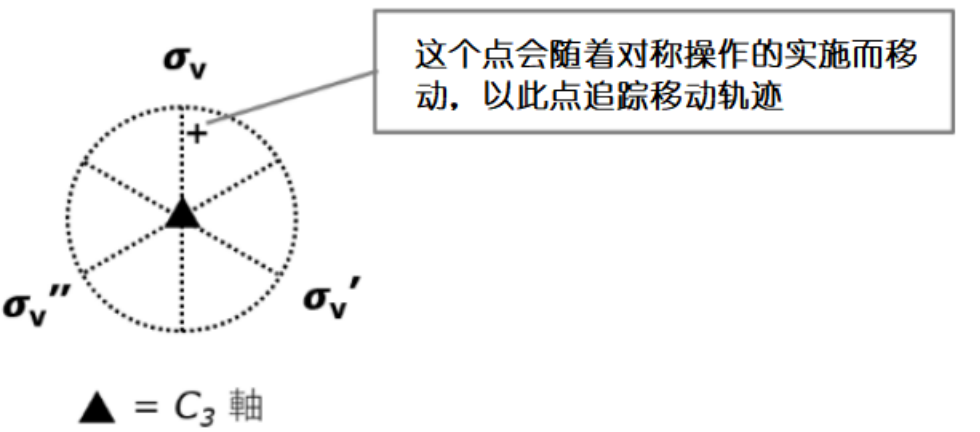
立体投影有助于理解对称操作的积。纸面上的物体用+表示，下方的物体用〇表示。黑色n角形代表C_n轴，白色n角形代表S_n轴（ C2和S2(=i)表示为椭圆）

有了立体投影图，我们来看看C₃操作后σv操作后会发生什么，+移动到了左下的位置。从起始位置直接移到终点位置的操作为σv’，所以C₃操作后再进行σv操作等价于一个σv’ 操作。用数学式表达为σvC3 = σv’  。要注意写法是σvC3，代表先进行的是C₃操作。

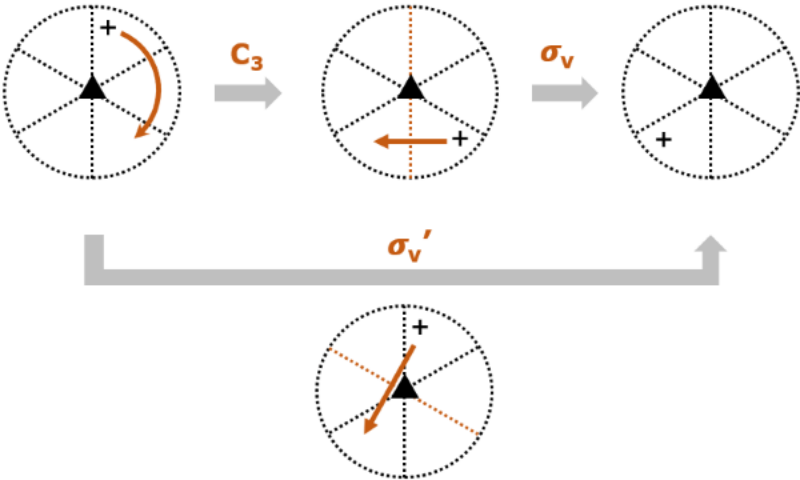
立体投影说明σv C3 = σv’

再举一个例子。刚刚的例子里“先进行C3再进行σv’ ”等于σv”。(σv’C3 = σv”)。如果没有C₃操作呢？“先进行σv再进行σv’”等于C32。(σv’ σv = C32 )。

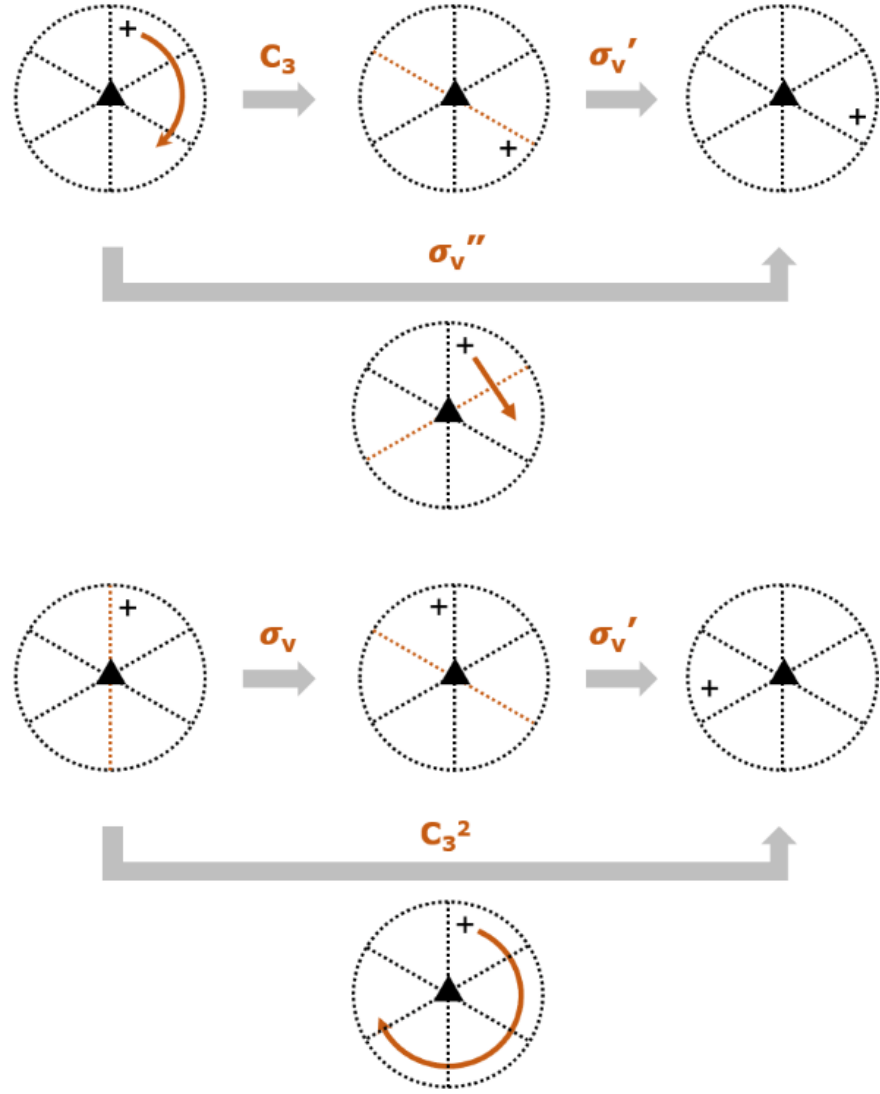
σv’C3 = σv”的示意图（上）和σv’ σv = C32的示意图（下）

这样的立体投影法可以用来计算一切对称操作的“积”。动脑不如动手，自己亲手画一遍胜过过目百遍。请读者在彻底理解了这个方法后再继续往下看。

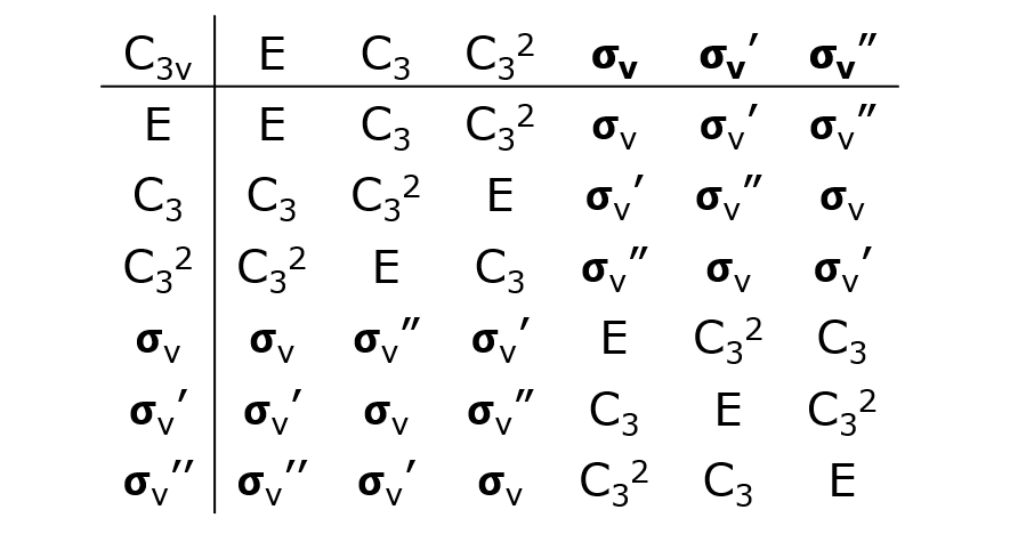
氨分子的对称操作的积表

通过立体投影法，我们可以填充满氨分子所有对称操作的积表。积表中所有的“积”操作都是氨分子原有的对称操作，换言之，对氨分子的任意两个对称操作求“积”并没有产生新的对称操作。故而群的性质一——闭集性成立。那存不存在单位元和逆元呢？单位元，即为恒等操作E。积表的每一行（或者说每一列）都有一个恒等操作E。也就是说每个元（对称操作）都有对应的逆元。顺便说一下，每行或每列的所有操作都是不重复出现的。

最后，确认这张积表满不满足群的最后一个性质——结合律。这需要考虑三个对称操作的“积”。比方说C32σv’C3 ，由上面积表里的结果可知C32(σv’C3) = C32 σv” = σv，C32(σv’C3) = C32 σv” = σv，所以我们可以说C32(σv’C3) = (C32σv’)C3 这个等式成立，但是只凭这个例子是不能说明结合律成立的一般性的。这里我们需要用到线性代数的知识了。

诸如旋转和反映的对称操作就要用矩阵表示了。矩阵的积对应的是对称操作的“积”。从这里开始我们就要启用矩阵的“积”来代替对称操作的“积”。首先将对称操作转换为矩阵，求矩阵的积，然后将结果再转换回对称操作。如果矩阵的计算过程符合结合律，那么对称操作的计算过程也同样符合结合法则。

至此，氨分子的所有对称操作集合 {E, C3, C32, σv, σv’, σv”}满足了群的所有条件：闭集性，结合律，存在单位元，存在逆元。

所有的分子对称操作的集合都是满足群的条件的。在分子的对称操作中，因为总有一点保持不动，所以分子对称操作的集合又被称为点群(point group)。使用点群来讨论分子的性质的时候可以暂时无视分子的化学性质(比如元素的种类)，可以只基于分子的形状给出定性结论(键的状态，振动)。

化学家，特别是结晶学化学家还需要学习平面群(plane group)和空间群(space group)。平面群和空间群中有螺旋操作和平移操作这样的平行移动操作，还有点群没有的操作。

群论的专门术语

从开头到现在，我们已经讨论了“群”很久了，下面我来科普一些群的相关专业术语以便读者阅读后续的文章，记不住没关系，等看到陌生的术语勤回来翻看就足够了。

• 一个群中元素的个数被称为阶(order)，用符号h表示。
• 如果一个群的操作的积是可交换的（AB=BA），那么这个群被称为阿贝尔群(Abelian group)。
• 由一个群的元素与它本身反复取积而产生的群称为循环群(cyclic group)。

这里有几点需要补充说明。首先群的成立条件不包括交换律。如果倒回去看氨分子的那张积表，积表对角线两侧并不是对称的：操作的先后顺序会影响“积”。先进行C3再进行σ，“积”为σ’，先进行σ再进行C3， “积”为σ”。因此，对点群来说交换律不成立，满足交换律不是群成立的必要条件。

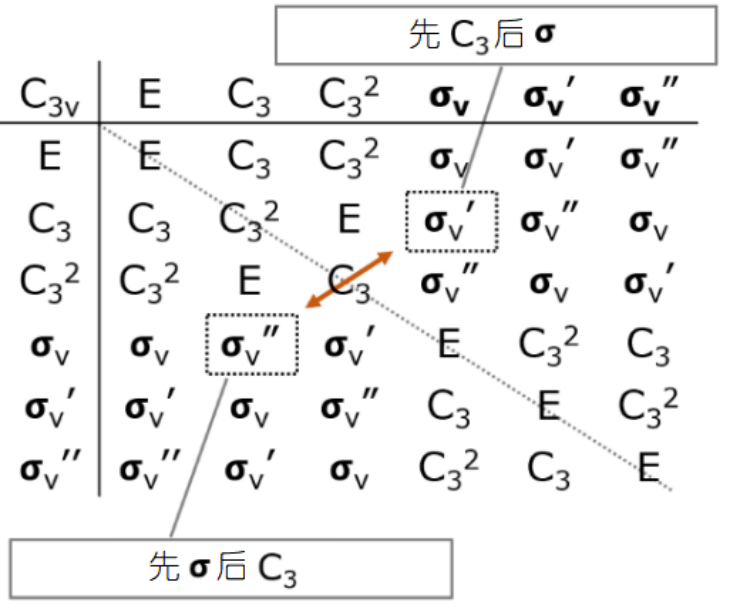
氨分子的对称操作的群不满足交换律，从这张表中我们可以看出对角线两侧的积不一样

其次，关于什么是循环群，在上文中出现过的群I= {1, i, -1, –i}。i的一到四次幂 (i2 = -1, i3 = –i, i4 = 1)可以构成群I的全部四个元素。循环群也是阿贝尔群。总的来说循环群的积是可交换的。

总结

本文的重点总结如下

群是赋予“积”数个定义时，全部满足以下条件的元素的集合

性质1：闭集性

性质2：结合律

性质3：存在单位元

性质4：存在逆元

如果分子的所有对称操作的集合满足以上四个条件，那么称这个集合为点群。

参考文献

1. 本記事の内容は主に次の書籍を読んで学んだ知識を利用しています. より詳細に学びたい人はこちらをあたるとよいでしょう. 値は張りますが, 下に Amazon のリンクも張っています: Cotton, F. B Chemical Applications of Group Theory, 3rdedition;Wiley.

本文版权属于 Chem-Station化学空间， 欢迎点击按钮分享，未经许可，谢绝转载