本文来自Chem-Station日文版 なぜ電子が非局在化すると安定化するの?【化学者だって数学するっつーの!: 井戸型ポテンシャルと曲率】やぶ

翻译投稿 炸鸡 校对 HaoHu

本篇内容为了从数学角度来揭开量子化学的原理，选择以最简单的一维深阱里的薛定谔方程作为讨论对象。薛定谔方程很好地结合了波函数的曲率和能量，从薛定谔方程出发我们可以得出量子力学里面粒子的能量取值离散的原因以及轨道能级变高轨道的节点就增加的原因，进一步明白为什么电子会离域或是定域。

前情回顾：与时间无关的薛定谔方程

在上一回中我们讲到，在假定波函数表示的是驻波的前提下，怎么推导出教科书上的“与时间无关的薛定谔方程”。

在这个薛定谔方程中，m表示的是粒子的质量，ħ是普朗克常量（一个比值常数），E表示的使粒子的能量，Ψ（希腊字数，读音为pusai）表示的是波函数。Ψ的括号内的r表示的是粒子的坐标 r = (x, y, z) 。化学家常常利用与时间无关的薛定谔方程来求解电子的波函数或电子的能量。因为波函数与电子的存在概率有着密切关系，所以波函数又被称为电子的轨道，波函数对化学家来说有着举足轻重的意义。
所以今天我们以最简单的模型——一维封闭深阱里的粒子作为例子。这是量子力学里最简单的一个系统。在求解该系统下粒子的薛定谔方程时，我希望读者们都能注意到化学课本上提到的“量子学规律”。

一维深阱式系统是个什么样的系统呢？

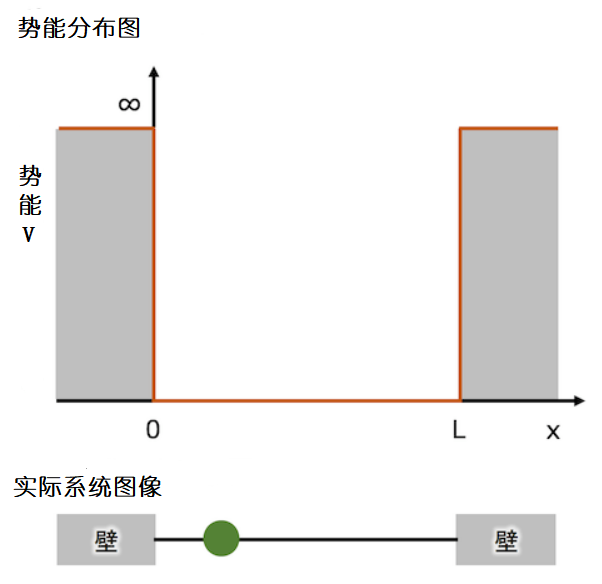
在一维深阱式系统里，粒子只存在于X轴上，且在X轴上粒子的势能都为0。在X轴以外的地方，粒子的势能都为无穷大，且粒子无法穿透墙壁。如果在X轴上画出势能的大小曲线，这个曲线就会呈现一个像深阱的样子。

深阱式中的势能曲线（上面一幅图中的橘色的曲线）和实际中的系统（下面一幅图）。

这个系统内薛定谔方程有什么样的形式呢？

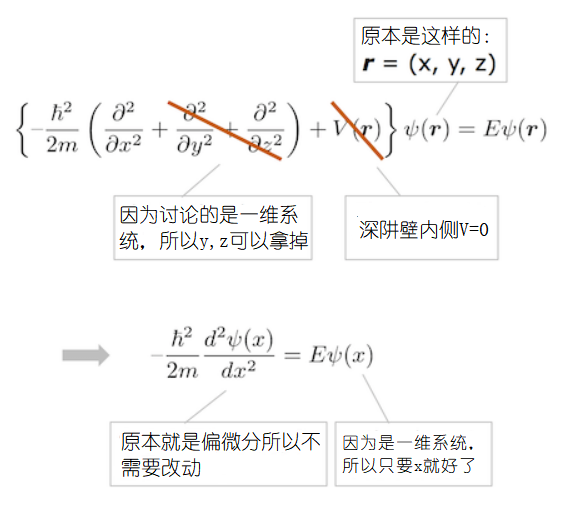
由于我们假设阱中的势能为零，并且现在我们仅考虑一维（X轴）的情况，所以深阱中的薛定谔方程应如下所示。

我来解释下这个薛定谔方程为何会和文章一开头给出的薛定谔方程不同。因为现在我们考虑的是一维即X轴系统的情况，所以波函数Ψ的自变量（括号中的）不是r=(x,y,z) 而只有x。不仅如此，因为自变量只有x，所以微分不是偏微分 ，而是常微分 （当自变量有2个以上时，才需要考虑偏微分）。

因为粒子在深阱中的势能为0，所以粒子的能量就只有动能了。因为粒子的动能大小恒为正，所以E > 0 。但具体E多大现在我们还不知道。所以接下来我们要通过计算求解E的大小。

这个薛定谔方程有什么实际意义吗?

对于这个一维深阱里的薛定谔方程，我们可以做出如下解读：

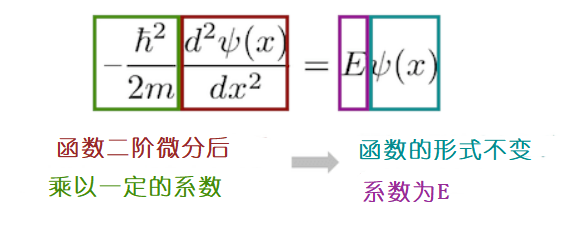
一个函数Ψ二阶微分后乘以一定的系数，得出的结果为这个函数的E倍。有什么样的函数Ψ和E满足这样的条件呢？

如果我们能找到满足上述条件的函数Ψ和系数E就能求得这个薛定谔方程的解了。

那么我们怎样才能找到满足上述条件的函数Ψ和系数E呢？

有些数学好的童鞋可能会想到“二阶微分后函数形式不变的函数，那就是三角函数和指数函数了”。这个思路是正确的，我们把波函数假设为三角函数或复数指数函数就可以解出这个薛定谔方程了。具体来说，我们将集中在利用薛定谔方程的左侧代表函数曲率这一事实来半定性地预测波动函数的形状。感兴趣的童鞋可以参考量子力学的书籍上的解法。本篇内容的目的是从等式的性质出发阐明量子力学原理，故解法部分不做详细说明。

“等式左边表示函数的曲率”这是为什么？

我们来把一维薛定谔方程稍微变形一下吧。把左边的系数全部挪到右边，那么左边就只剩下关于x的二阶微分了。

但是这个薛定谔方程的本质是没有改变的。我们可以这样看待我们改造后的式子：

对波函数求二阶微分后，波函数的形式竟然没有改变，并且前面多了个有关E的系数。 有哪个波函数和E是满足这样的条件的呢？

在这里我们稍做停留，仔细思考下：波函数的二级微分表示什么意思呢？我们都知道函数的一阶微分（即导函数）表示的是这个函数上的点对应的曲线的切线的斜率，那么函数的二阶微分（对一阶微分再求微分）表示的是函数上的点对应的曲线的切线斜率的变化率，用数学术语来讲二阶微分表示的是函数的曲率（表示函数曲线的弯曲程度）。
让我们来复习下高等数学里学过的函数的曲率吧。让我们先把目光集中在下图中凸起的（左半边）的曲线的弯曲程度。曲线上的点对应的切线斜率一开始为正数，随着x的增加逐渐变小，变为0，变为0时切线就变成水平了，然后切线斜率继续变小，变成负数。总的来说，在向上凸起的函数曲线里，曲线的切线的斜率的变化率是负的（即曲线的切线的斜率在不断变小），所以我们说对于左半边曲线而言，它的曲率为负数。同理，在右半边的向下凸起的函数曲线中，函数曲线的切线的斜率的是在不断变大的，即切线斜率的变化率为正。所以对于右半边曲线而言，它的曲率为正数。所以我们可以总结出这样一条规律：函数曲率为负数时，函数的曲线就呈向上凸起状，函数曲率为正数时，函数的曲线就呈向下凸起状。

函数的二阶微分（曲率）的意义。二阶微分（曲率）为负时，代表函数曲线是向上凸起的，二阶微分（曲率）为正时，代表函数曲线是向下凸起的。

函数的曲率和薛定谔方程是解有什么关系呢？

通过讨论函数的曲率，我们就能预测波函数的大致形状。在加上波函数的临界条件，就不难求出系统的波函数和E了。下面让我详细讲解。
让我们从曲率的角度来重新审视这个薛定谔方程。

• 波函数的曲率与粒子的能量E，Ψ函数的值成比例（规则1）

因为E表示的是粒子的动能（一维系统里我们假设粒子势能为0），所以E为正值，等式右边里面的质量m和普朗克常量ħ也都取正值。又因为等式右边有负号，所以等式右边的系数部分恒为负数。这意味着：
• 波函数的曲率的正负情况和Ψ函数的值相反（规则2）
有了关于函数曲率的信息我们可以大致推测出波函数的形状了。
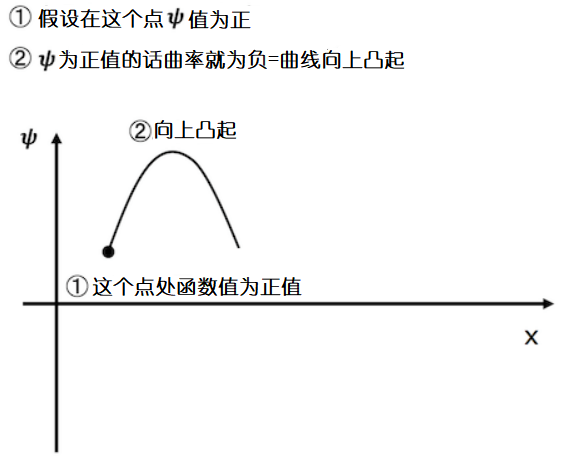
比如，当波函数在某个区间内，波函数值为正值时，根据规则2，函数在这个区间内的曲率 为负值。假设函数曲线的起点在第一象限，先向上攀升然后下跌，函数曲线整体呈向上凸起状。

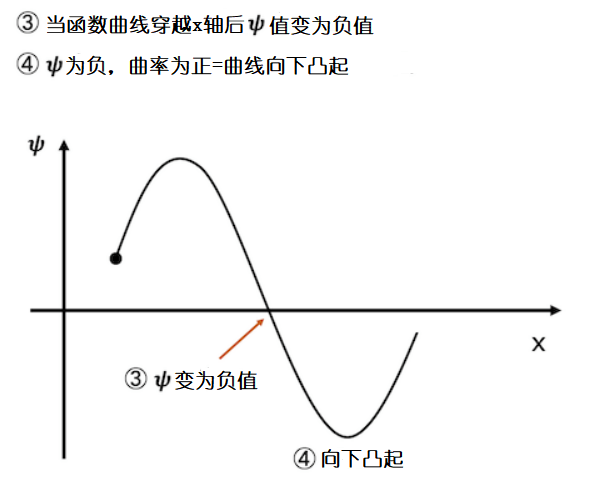
这个向上凸起的函数曲线继续下跌，曲线总有一个时刻穿越x轴变为负值。波函数的值一旦变为负值，根据规则2，曲率 就成为正值。所以函数曲线呈向下凸起状。因此波函数变为负值后，波函数曲线呈向下凸起状。

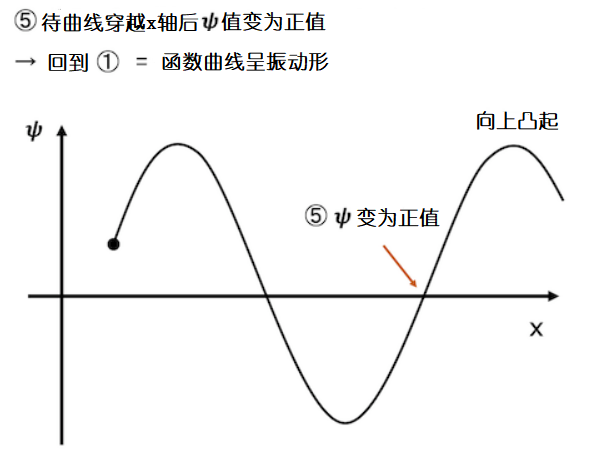
向下凸起的函数曲线总有一个时刻穿越x轴，穿越x轴后函数值变为正数，根据规则2，曲率变为负数，函数曲线会再次变成向上凸起的样子，然后某个时刻波函数又再次变为负值……照此往复循环。这样我们就得到了波函数的大致样子。

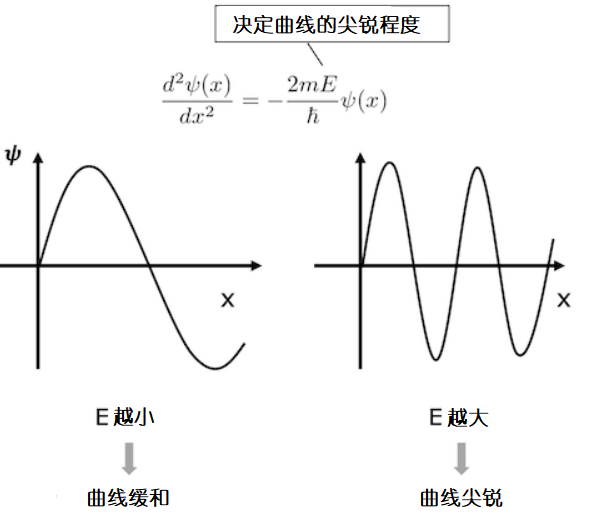
讨论完形态，让我们来讨论函数曲线上升的缓急程度。根据规则1“波函数的曲率与粒子的能量E，Ψ函数的值成比例”，粒子的动能越大，波函数的振动就越快速。换言之，粒子的动能越大，波函数的曲线就变得越尖锐，变化的也更快（注意波函数的振幅不发生变化）。

预测的函数真的是薛定谔方程的解吗？

难道只要函数图像像这样的函数就可以了吗？不是的。今天我们要面对的是一维深阱式系统，在两端阱壁上时波函数必须为0。为什么在阱壁两端波函数的值得为0呢？这要从波恩定则和微分方程的性质说起。
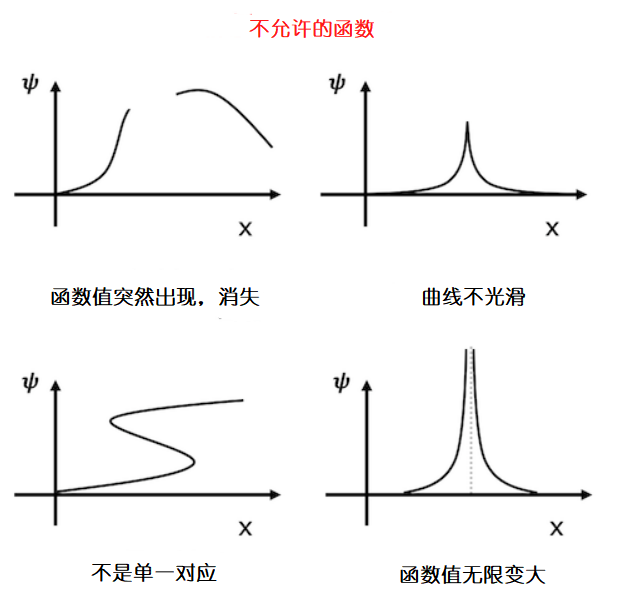
根据波恩定则，波动函数的绝对值的平方指示着粒子的存在概率。波动函数必须是平滑，连续的曲线，因为粒子不可能突然消失或出现在某些边界处。比如说波函数的值不可能突然从0变成0.5或0.8。用数学的话来说，波函数必须是连续的。并且粒子在一个地方的存在概率不可能有两个值，所以横坐标上一个x的取值只能对应一个波函数的值。另外，还有一个条件是函数不能无限期地发散，因为所有区域中的存在概率之和必须为1（边界）。综上所述，波函数必须是单对应，有边界且连续的。

物理上不允许出现的波函数。波函数必须是单对应，有边界且连续的。

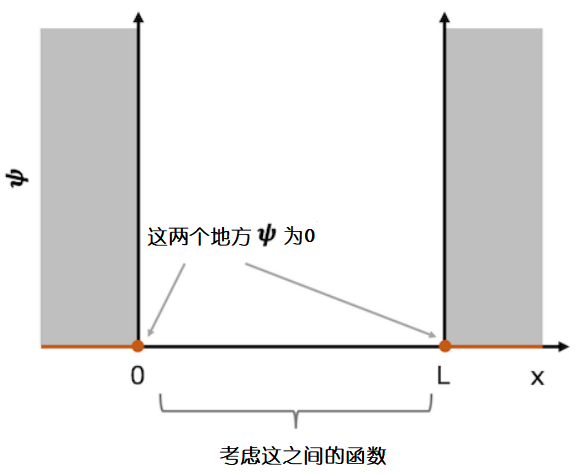
阱壁外面的势能是无限大的，所以假定粒子是不会穿破阱壁的。因此阱壁外的波函数的值为0。但是波函数又必得是连续的，意味着波函数不能突然变为0。在这种情况下，波函数在阱的左端必须（x = 0）为零，波函数在阱的右端也必须为零（x = L）。很好地满足这两点需求的函数将被认为是该系统的波函数。

深阱系统内的边界势能情况。因为粒子在深阱外的存在概率为0，又要满足函数是连续的，所以深阱两端的波函数的值必须为0。

那么到底什么函数才是真正的解呢？

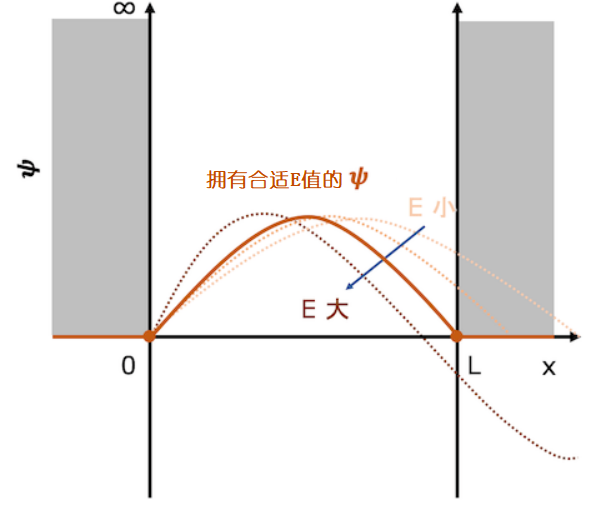
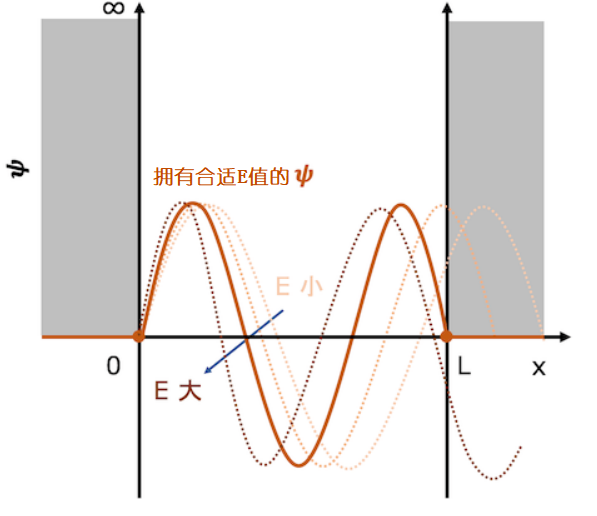
想象一下函数的曲线先是向上凸起的曲线（波函数的值为正，函数曲线是呈向上凸起状的）。曲线的缓急程度由粒子的动能决定（深阱系统内粒子势能为0，所以粒子动能等于总能量），粒子的动能越大，曲线就越陡。首先我们想象粒子的能量很小，那么粒子的动能也很小，则波函数的曲线会比较缓，延伸到阱壁右端后函数值不能立马变为0，这样的话函数必得穿透阱壁（下图中橙色虚线）。这样的函数曲线是满足不了我们预先设立的边界条件的，所以这样的波函数及其能量并不是一维薛定谔方程的解。
那么粒子的动能E稍微大一点的话行不行呢？即曲率变小一点点。当E在一点点变大时，函数曲线正在发生变化直到出现一条曲线能满足左右临界条件（见下图橙色的实线）。这条橙色实线表示的函数曲线正是我们想要的，这个波函数及其对应的能量E也就是一维薛定谔方程的解。但是当E不断变大，函数曲线会渐渐提前穿越X轴，便不能满足边界条件（见下图红色虚线）。

当粒子能量逐渐增大，满足条件的波函数曲线会渐渐浮出水面。

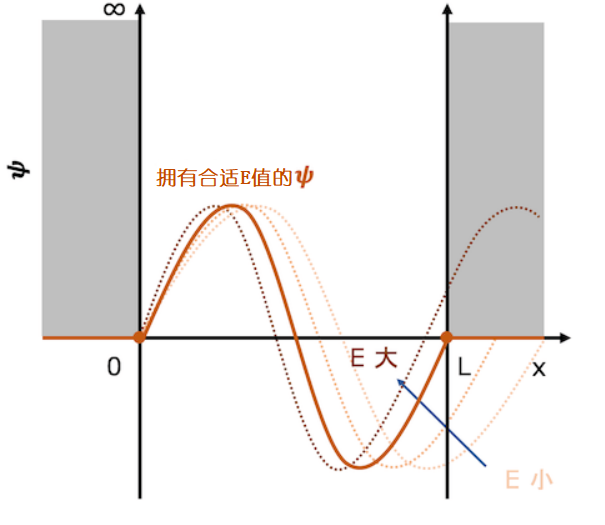
那如果E进一步增大呢？会发生什么呢？如前所述，在波函数为负值的区域中，波函数向下凸出。因此，如果增大E，曲线就变得更锐利，则通过一个波形的振动，阱壁的两端被连接起来。但是，如果曲线变得比这更紧密，则波函数将再次取正值，并且阱壁的两端将又不会被连接起来。

当能量继续增大时，又会出现一个符合条件的波函数曲线。

E值继续增大，波函数取正值时，函数曲线呈向上凸起状。因此当E值持续增大到一个值时，又会出现一个曲线连接阱壁两端，这个波函数也是物理上允许的一个解

当能量持续增大时，又会出现一个符合要求的波函数。

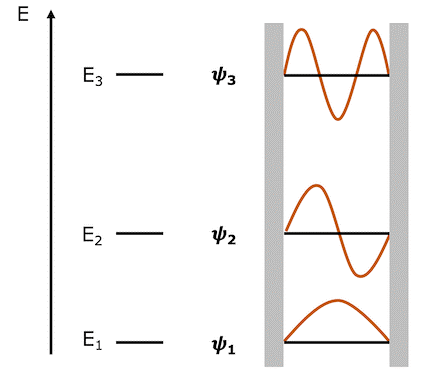
下图展示了我们已经讨论过的几种解。下图表示相应的波函数仅在一定能量下存在。顺便说一句，通常将数字1作为最低能量值及其对应的波函数的下标，以此类推，数字2就作为比最低能量高一点的能量值及其对应的波函数的下标。这些下标称为量子数。

解开这种非现实存在的系统的薛定谔方程有什么实际意义吗?

通过定性求解薛定谔方程，我们能得到量子力学上两个重要的结果。第一个：粒子的能量不能任意取值，只能在间隔特定值取值。也就是说，在量子力学的世界里，能量不是连续的。第二个：随着粒子能量的增加，能量的取值所对应的波函数的节点也会增加。让我们接下来慢慢道来。

粒子的能量是离散的，这为什么奇怪呢？

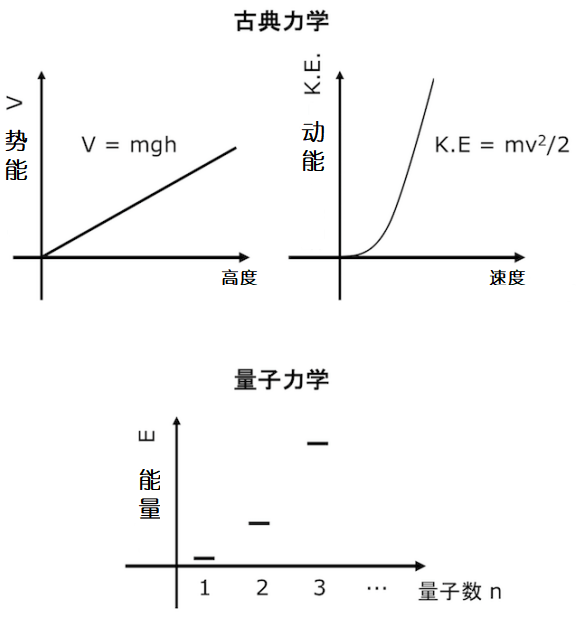
这与牛顿力学中的连续能量相反。比如在牛顿经典力学中，动能的公式为1/2 mv2。物体运动速度不同我们就能收获不同的动能值。势能的公式为V = mgh，物体被持续举高，物体的势能就会成比例地变大。但是如我们上文里所讲的，在量子力学的世界里，粒子的能量是不能连续变化的。

古典力学和量子力学的能量的取值上的差异

为什么量子力学中能量是离散的呢？

这要从物理上设定的边界条件和数学计算说起。学过高等数学的都知道，当任意积分常数出现在微分方程中时，微分方程会有无数个解。但是，边界条件的存在限制了物理上有意义的解的个数。结果，只有有限的波函数可以满足边界上的连续性条件，并且仅允许与该函数相对应的能量作为粒子可以吸收的能量。
考虑原子轨道的时候也是这样的。比如对于球形的s轨道而言，电子在原子核附近的存在概率不为0，但是在距离原子核无限远的地方的存在概率为0。读者可以这样理解：在距离原子核无限远处，Ψ = 0，这就是边界条件。

“波函数的节点”是什么？

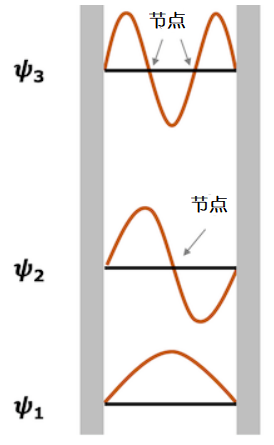
波函数的节点指的是波函数值为0的点或区域。物理上意味着粒子存在概率为0的区域。

深阱型的波函数的节点。

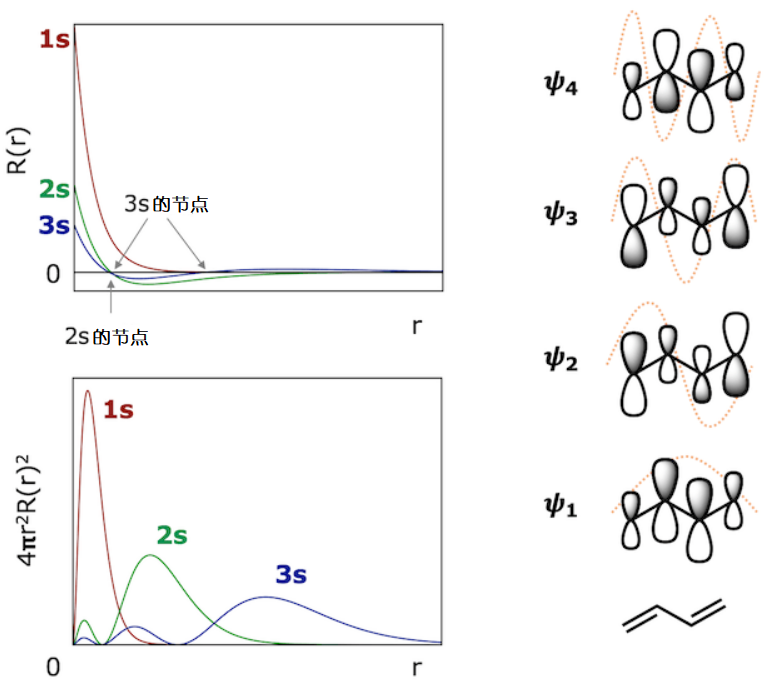
在深阱型系统的这个例子中，我们看到相应的波函数节点随着粒子能量的增加而增加。该规则是个一般规则，不仅适用于深阱型系统，而且还适用于原子轨道和分子轨道。1s轨道是一个原子的轨道，没有节点，但是2s轨道有一个节点，而3s轨道有两个节点。另外，在共轭多烯的π轨道中，随着分子轨道的能级的升高，节点数随之增加。结点的数量随着粒子能量的增加而增加的事实意味着：随着能量的增加，波函数的曲率变大，因此在波函数穿过水平轴后必须满足边界条件。

（左）氢原子的1s，2s，3s轨道的径向波函数（左上方）和径向分布函数（左下方）。径向分布函数表示在距原子核r〜r + dr的微小壳层中发现电子的概率。如果半径较小，则壳的体积较小，因此，即使波函数本身在原子核附近较大，径向分布函数也会为零。（右）1,3-丁二烯的π轨道中的橙色虚线表示与深阱型系统的对应关系。

如果深阱变宽的话，薛定谔方程的解该如何变化？

波函数的轮廓几乎不变，但是每个能级的能量降低了，并且能级之间的能量差减小了。接下来让我们详细说明。
首先要记住的是，在前面的示例中，即使在最低能量下，粒子也具有动能。对经典力学而言静止的粒子没有动能，因此最低的能级为零。总之对经典力学而言，动能可以为零。

但是对于深阱型系统而言，粒子的动能为0的解是不存在的。因为波函数曲线的弯曲程度（曲率）指示着动能的大小。如果用完全不弯曲的直线（即曲率为0）连接阱壁的两端，则波动函数在整个深阱中必须一直为零。这意味着整个空间里没有粒子存在。要想两端波函数值为0同时中间部分不为0的话，波函数的图像就必须是一条曲线。所以我们说“当粒子在深阱中时，它的动能一定不为0”。
现在我们开始讨论深阱变宽的情况。深阱变宽，连接边界的波函数曲线将会变缓。也就是说曲率变小，那么电子的动能也会变小，电子也会更加趋于稳定化。

深阱变宽的话，函数曲线就会变得缓和，整个系统的动能就会降低。

共轭π电子会更稳定的原因就是这个。因为π电子一旦形成共轭体系就相当于“阱”变宽了。不光形成π电子共轭体系能降低电子能量，成键也能降低电子能量，这也是因为“阱”变宽会引起电子能量降低。例如，氢离子它的化学键都被当作是分子轨道，所以氢离子一直被当作最简单的系统被研究^[4]。在很多大学教材里都提到“两个氢粒子之间共享电子，电子像胶水一样把两个氢离子粘在一起”。但实际上却不完全如教科书上所说，因为我们还需要考虑库仑力和电子离域的因素^[4]。
本次文章的标题《为什么电子要离域或定域？》的答案就是“当电子的运动领域变广后，为了满足边界条件，波函数的曲率就会降低，从而电子的能量就会降低”。

总结

在本篇内容里，我从“薛定谔方程是波函数和曲率的关系式”这一视角出发预测波函数的形状，进而通过设置边界条件而得到随着轨道能量增大波函数的节点就增加这一结论。今天我没有用到数学计算，而是掺杂着数学思维来理解量子力学原理和从更宏观角度解释化学现象。下一次开始，我将用变分法求解氢离子的分子轨道，并用数学来讨论分子轨道方法的基本原理。

参考文献

1. Atkins, P. W. ; de Paula, J. C. Physical Chemistry, 10th Edition, 2014, Oxford University Press.
2. DeKock, R. L.; Gray, H. B. Chemical Structure and Bonding, 1980, University Science Books.
3. 九鬼導隆 「量子力学入門ノート」2019, 神戸市立工業高等専門学校生活協同組合.
4. Ruedenberg, K.; Schmidt, M. W. J. Phys. Chem. A 2009, 113, 10, 1954–1968. DOI: 10.1021/jp807973x