本文来自Chem-Station日文版 ラマン分光の基礎知識 ferrum
翻译投稿 炸鸡 校对 白菜猪肉馅
当光射入物质中时光会发生散射，散射光中有一部分光与入射光的能量有差异。我们把这种现象称为拉曼散射。拉曼散射作为光谱学的一种分析手法使我们可以依据入射光与散射光之间的能量差异获得与分子振动频率的相关信息。
拉曼散射是什么
光的散射（scattering of light）是指光通过不均匀介质时一部分光偏离原方向传播的现象。当用高强度的光（比如激光）照射一张表面粗糙的纸，我们观测到从照射点附近发出的散射光就知道有光照射到纸上了。
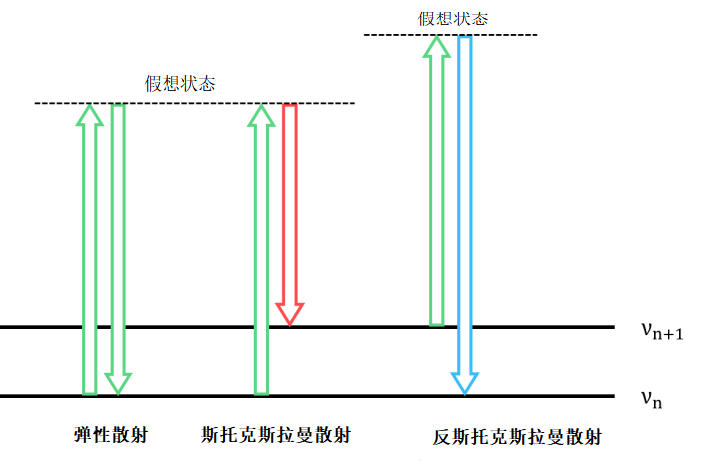
大部分散射光的波长和入射光的波长一致（例如弹性散射，更严谨的说是瑞利散射），同时也有小部分的散射光与入射光有小量的能量差异。这一现象最早由C. V. Raman和K. S. Krishnan发现，故称为拉曼散射。拉曼散射中的散射光与入射光的能量差异起因于分子振动。分子的振动中也存在能级，振动的量子数变化的话，分子的能量也会随之变化。我用一张能量示意图简要说明下吧（下图）！弹性散射是指分子从某一振动量子数被激发到一个能级又返回到同样的振动量子数的散射，分子返回到和开始的振动量子数不一样的振动量子数的散射叫拉曼散射。拉曼散射中，分子返回的振动量子数比开始的振动量子数高的散射叫斯托克斯拉曼散射，分子返回的振动量子数比开始的振动量子数低的散射叫反斯托克斯拉曼散射。
拉曼散射光谱概述
当强光照射分子时，散射光中有一部分光会与入射光的波长不一致，我们能根据这个差值计算出分子振动的能量。具体计算公式如下，入射光的角振动频率用Vin表示，拉曼散射光的角振动频率用Vout表示。
ΔE=h(Vout-Vin)(1)
因为弹性散射的缘故，散射光大部分与入射光波长一致，这种情况，ΔE=0不会妨碍解析。如果只关注零点振动（n=0）和其上1个振动（n=1），理论上只需使用能量比其能量差大的电磁波即可。下图是拉曼散射光谱，图谱正中间的那个强峰（拉曼位移为0）是入射光（由弹性散射引起的），两侧的是拉曼散射光的峰。在一个分子集合中，大多数分子处于基态振动水平，即大多数分子所处的能级都非常地低，所以一般来说斯托克斯散射的峰要比反斯托克斯散射的峰要更强。下图是硫磺的拉曼光谱图。根据公式（1）可知，当Vout-Vin≤0时，为斯托克斯散射，当Vout-Vin≥0时，为反斯托克斯散射。
[1] 引用
在最经典的非共振拉曼光谱中，中间状态的能量较高，并且为了达到低于电子激发态的能量，经常使用可见光。
拉曼振动光谱示例
[2]引用
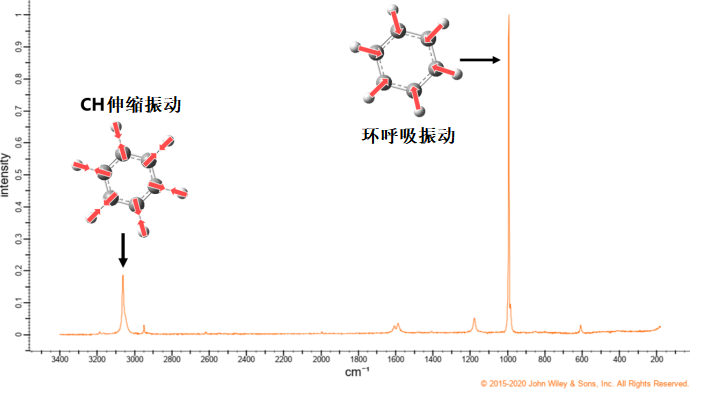
从拉曼散射光谱上的拉曼位移（入射光的能量改变的程度）能得到振动光谱。实际情况下，测定拉曼光谱时多数情况下只能得到振动光谱。这张图是苯环的拉曼振动光谱。
拉曼散射选律概述
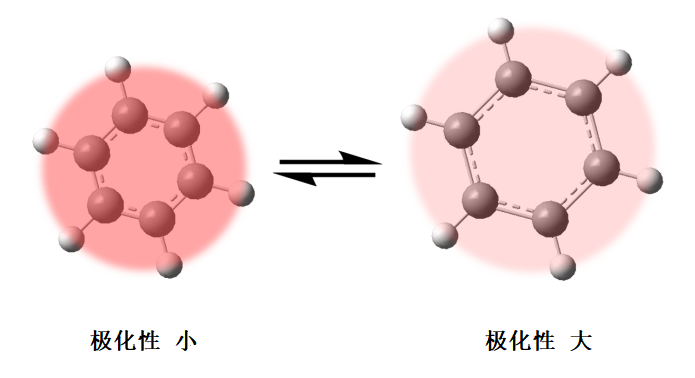
测定振动能级的光谱大致分为两种。一个是红外光谱（infrared: IR）还有一个是拉曼光谱。在红外光谱里一个光子激发一个分子到振动状态，我们称分子的这种振动模式是有红外活性的，在这种振动模式下，在平衡核坐标（即振动中的分子的时间平均核坐标，就是我们在纸上画的分子结构式的核坐标）中可以看到分子的偶极矩发生了变化。对于具有拉曼活性的振动模式而言，该振动模式下的平衡核坐标里的极化性（polarizability）（在物理学里，感受到外电场的作用，中性原子或分子会改变其正常电子云形状，衡量这改变的物理量称为极化性）会改变。极化的难易程度与电子的密度有关，电子密度越大，越难极化；电子密度越小，越容易极化。全是分子的情况下，分子在保持形状的前提下做扩张•缩小的振动运动，此时分子上的电子密度不可避免会变化，所以极化性也会随着变化。可以大致认为对称性高的分子的对称伸缩振动是具有拉曼活性的。例如，在苯的环呼吸振动中，由于在核运动静止时电子密度为最大或最小，因此苯环的振动是具有拉曼活性。
拉曼散射的选律的数学解释
接下来我会用数学公式来详细讲解选律。
在红外光谱（光直接激发分子振动或转动）中，电子跃迁的概率与
的平方成正比。，分别为初始状态和末状态的波函数，是偶极矩运算符。对于具有永久偶极矩（平衡核座标的偶极矩）的分子，由于振动，经常会发生变化，所以的值不为0。但是对于不具有永久偶极矩的分子，只有对特定的光电场方向，才会改变，只有在这种振动模式下才不为0，这种不具有永久偶极矩的分子才具有红外活性。
而在拉曼光谱中，应该考虑的是从初始状态到末状态之间的感应偶极矩的变化。感应偶极矩用P表示：
其中代表极化性张量。极化性张量是分子固有的2阶对称张量（对称矩阵）。
在这个对称矩阵里，有且这三组值互相相等。极化性这一参数表示极化的容易程度与电子密度之间的关系。一般来说，在电子密度高的状态下很难极化，但在电子密度低的状态下容易极化。感应偶极矩的变化是指极化率在平衡核坐标附近变化，这种振动会引发拉曼散射。例如，在上图所示的环呼吸运动中，在平衡核坐标附近可以看到极化性的变化。
那么极化性的变化怎么表示呢。让我们用平衡核坐标里的简正坐标表示：
简正模（简正模是一个振荡系统中所有部分都以相同的频率和相位以正弦函数形式运动的模式）指的是沿着这个简正坐标运动的原子核的运动模式，若要求分子具有拉曼活性，则作为简正模的的简正坐标必须满足以下条件：
只有满足（5）式，才会存在。感兴趣的读者可以翻看相关专业书籍的详细的记载。
共振拉曼效应
正如前文所说，散射光大部分为弹性散射光，拉曼散射比弹性散射弱。然而，通过使用接近电子激发跃迁能级的光作为入射光，可以将电子激发态作为虚拟的中间态。此时，偶尔可以观测到特定的对称振动模式及其谐波。这就叫做共振拉曼效应。另外，在共振拉曼散射中，其中间状态与电子状态的哈密顿算符有关，因此，即使在非共振拉曼散射中被禁止的振动模式有时也能被观测到。
参考文献
Raman. C. V.; Krisgnan K. S. Nature, 1928, 121, 501-502. DOI:10.1038/121501c0
相关链接
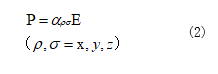
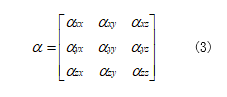
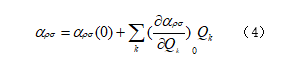
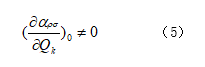
No comments yet.