概要

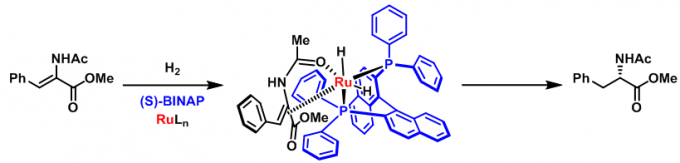
手性的概念是在1893年由英国化学家L. Kelvin（W. Thomson）提出（在电子发现的四年之前）。L. Kelvin指出对于任意的几何图形或点群及手性分子而言，如果对它们进行镜面反映操作之后，产生的镜像不能与它本身相一致，则该物体就是手性的。将这一概念应用于有机化学中，便开创了对手性分子的研究。从那时开始，化学家们普遍认为分子的手性纯粹是分子的一种几何性质。因此，在手性化学，尤其在对映选择性合成设计的相关研究中，普遍认为反应的对映选择性受到分子内几何因素（立体效应）的控制。在解释所得反应产物的绝对构型时，通常都只是构建一种立体效应有利的过渡态（Fig 1）。例如，我们所熟知的Noyori不对称氢化反应。

Fig 1. Noyori不对称氢化反应

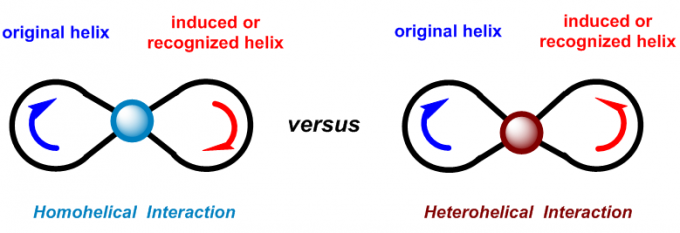
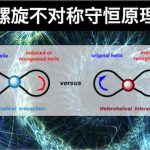
虽然有时也会结合诸如氢键、π-π堆积等电子因素进行考虑。然而，在实验中已经发现有许多反应，所生成产物的立体化学不仅无法根据立体效应进行合理的解释，甚至还会与立体效应相矛盾。因为上述模型中均未考虑到电子效应在控制反应对映选择性的过程中可能更加重要。美国Columbia大学的青年化学家王智刚教授认识到电子效应在手性分子相互作用中的重要性，以手性分子光学活性的螺旋模型为基础，提出了分子手性相互作用的螺旋电子理论（helix electronic theory）。该理论将手性分子分为左手螺旋（Light-Handed Helicity，LHH）与右手螺旋（Right-Handed Helicity，RHH），而手性分子的螺旋特性可十分方便地根据手性分子中基团的极化性顺序进行判断。 认为手性分子间的相互作用只存在同螺旋相互作用（homohelical interaction，指具有相同手性特性的螺旋间的相互作用）与异螺旋相互作用（heterohelical interaction，指具有不同手性特性的螺旋间的相互作用）。同时，作者提出了物理螺旋（physical helix）与几何螺旋（geometrical helix）这两个新的概念来代替之前化学家们普遍使用的电子效应与立体效应的概念。指出在不对称诱导过程中，几何螺旋与手性反应物几何形态的不对称性有关；物理螺旋在不对称诱导过程中表现为一种精细的电子控制，而不受分子立体大小的控制。不对称诱导过程中，物理螺旋所起的作用更为重要，上文中提到的同螺旋与异螺旋相互作用中的螺旋便是指物理螺旋，而非几何螺旋。

Fig 2. 同螺旋相互作用与异螺旋相互作用（小球表示结合在一起的螺旋之间的相互作用）

根据Tinico与Woody提出的螺旋中的电子模型（Electron-on-a-Helix Model), 同螺旋与异螺旋相互作用的能量（Eq. 1）如下式所示：

E_homo=h²n²/8m_eff(k+k’)²[(a+a’)²+(b+b’)²]

E_hetereo=h²n²/8m_eff(k-k’)²[(a-a’)²+(b-b’)²]

Eq. 1. 同螺旋相互作用与异螺旋相互作用的能量表式

由上式可以看出，同螺旋相互作用的能量要低于异螺旋相互作用。因此，手性分子间的相互作用中，同螺旋相互作用是有利的，即螺旋不对称守恒原理。作者将这一原理应用于不对称氢化反应、不对称Heck反应、CBS还原、Sharpless-Katsuki不对称环氧化、不对称硫醚氧化、不对称共轭加成、不对称自由基反应、动力学拆分等过程中产物立体化学的预测以及手性HPLC中的手性识别。发现螺旋不对称守恒原理不仅与之前化学家广泛应用的基于立体效应进行的预测具有优良的一致性，还可以解释那些应用立体效应理论无法解释，甚至出现相矛盾的实验结果。更为重要的是，与基于立体效应的模型相比，该理论使不对称催化反应相应目标产物绝对构型问题的探讨上大大简化。这一理论对于手性分子以及复杂天然产物的合成设计具有指导意义，为不对称催化反应的研究开辟了捷径。下篇文章小编将介绍各种类型的手性分子的螺旋特性的判断方法。

参考文献

1. Thomson, Baltimore Lectures on Molecular Dynamics and the Wave Theory of Light, C. J. Clay & Sons, London, 1904. Appendix H, p. 602.
2. J. Lough, I. W. Wainer, Chirality in Natural and Applied Science, CRC Press, New York, 2002.
3. N. Jacobsen, A. Pfaltz, H. Yamamoto, Comprehensive Asymmetric Catalysis, Springer, New York, 1999.
4. M. Rouhi, Chem. Eng. News., 2003, 81, 34. doi: 10.1021/cen-v081n039.p034.
5. Z. Wang, Mendeleev Commu. 2004, 244-247. doi:10.1070/MC2004v014n06ABEH002051.
6. J. Caldwell, H. Eyring, The Theory of Optical Activity, Wiley, New York, 1971.
7. H. Brewster, Top. Steroechem. 1967, 2, 1. doi: 10.1002/9780470147115.ch1.
8. H. Brewster, Top. Curr. Chem. 1974, 47, 29. doi: 10.1007/3-540-06648-9_8.
9. Giri, D.Z. Wang, P.K. Chattaraj, Tetrahedron, 2010, 66, 4560-4563. doi: 10.1016/j.tet.2010.04.055.
10. Tinoco Jr., R. W. Woody, J. Chem. Phys. 1964, 40, 160. doi: 10.1063/1.1724854.
11. Z. Wang, Tetrahedron, 2005, 61, 7125-7133. doi:10.1016/j.tet.2005.05.058.
12. Z. Wang, Chirality, 2005, 17, S177-S182. doi: 10.1002/chir.20140.
13. Z. Wang, Tetrahedron, 2005, 61, 71. doi: 10.1016/j.tet.2005.05.059.
14. Gilat, Concepts in Chemistry: a Contemporary Challenge, Research Studies Press, Taunton, 1996, Chapter 10.

本文版权属于 Chem-Station化学空间， 欢迎点击按钮分享，未经许可，谢绝转载！