译自Chem-Station网站日本版 原文链接:果たして作ったモデルはどのくらいよいのだろうか【化学徒の機械学習】
翻译:炸鸡
在上一回《从零开始了解机械学习【化学学生的机器学习】》中我们简单介绍了机器学习以及它在化学研究上的应用。今天这篇科普将会为大家介绍在机器学习中是如何评价机器建立的模型是否准确。本次介绍的机器学习仅限于监督学习。(不了解监督学习是什么的读者可以参考上一期)
模型到底指的什么?
上一回中介绍监督学习的时候,我用了“模型”一词,这里我想正式指出“模型”到底指的是什么。

模型和各变量的关系1
向函数y = f(x)输入值x,就会得到输出值y,那么我们可以说函数y = f(x)是一个模型2。x与其说是一个数字,不如说是一个矩阵。如果输出的y是离散的,输出变量则被称为标签3。
性能指标
在评价计算机经过机器学习后建立起来的模型时常会用到性能指标。而分类和回归分析的性能指标有所不同。
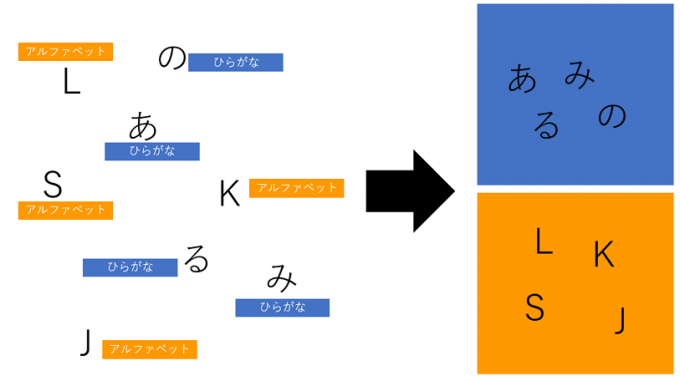
分类
分类的目的是训练计算机能够正确地将多个数据一一归类到多个类别,分类训练时的输出变数y是离散的。经过分类训练,机器多是判断输入值是属于两类中的哪一类:比如是属于猫还是狗,有没有特定的功能(active或inactive)。首先介绍两个针对机器建立的分类模型的评价标准。
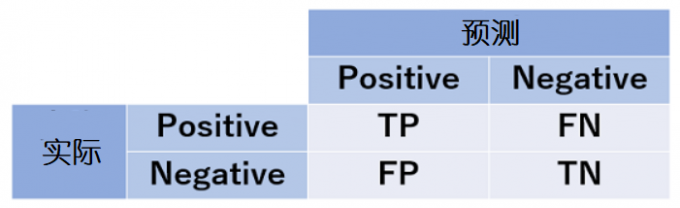
首先我们把机器的预测结果与实际结果的关系总结为以下四类。
将预测是阳性的﹑实际也归为阳性的归为真阳性(True Positive)
将预测是阳性的﹑实际是阴性的归为假阳性(False Positive)
将预测是阴性的﹑实际是阳性的归为假阴性(False Negative)
将预测是阴性的﹑实际也归为阴性的归为真阴性(True Negative)
混淆矩阵尽管能很好地对机器所建立的分类模型做出评价,但是很难与机器建立的其他模型做比较。所以这次来介绍四个将性能具体数字化的指标。
准确率(Accuracy):此值越高说明机器建立的模型能更准确地对输入变数进行分类4。
评价模型时有时会采用表示是否分类正确的准确率(Accuracy)作为评价指标,但是只依靠准确率来判断模型的精确度是不够的。
举个具体的例子吧:假设令机器对100张猫和狗的照片判断哪一张照片是猫,哪一张照片是狗,这100张照片里有92张照片是狗。在这种情况下我们靠准确率(Accuracy)来评价模型可不可行呢?如果机器对这100张照片全部做出归类为狗的判断,那么准确率高达92%。人们既定的思维是准确率越高这个模型就越好,但事实不尽然,只能单一输出的模型很难算得上是一个好模型。像此例一样,提供的数据集本身就存在偏差的情况不在少数,所以我们还需要借助准确率以外的指标来评价模型。
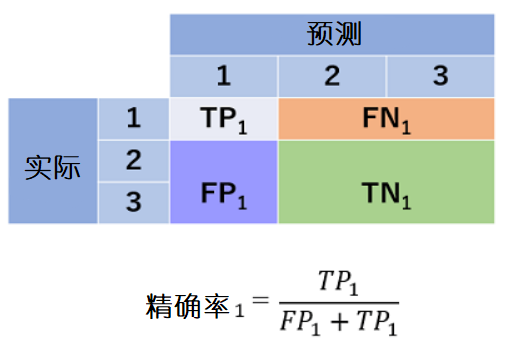
精确率(Precision):做出的全部“Positive”判断个数中与实际情况一致的个数所占的比例5。
召回率(Recall):做出“Positive”判断中与实际情况一致的个数占实际情况的“Positive”个数的百分比5。
F值,有时被称为F1或F-measure。精确率和召回率在某些情况下是矛盾的,F值是一个能很好平衡二者的指标。F值越高说明准确率和召回率之间没有大的偏差。
其他的评价指标如ROC曲线和AUC在这里就不赘述了。
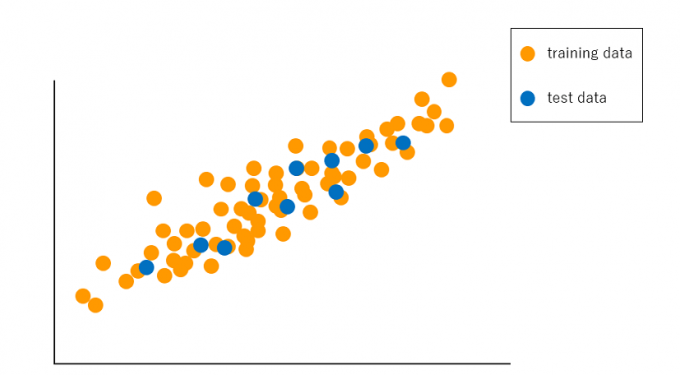
回归
当让机器进行回归类型的机器学习时,目标是输出值y接近于实际测量值,输出值y是一组连续值。
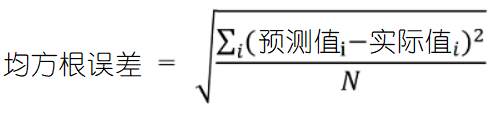
均方根误差 (Root Mean Square Error, RMSE)代表误差,均方根误差越小越好。
平均绝对误差(Mean Absolute Error,MAE)和RMSE差不多,也是越小越好,
决定系数(R2),这个指标在Excel中设定近似曲线就会出现。表示数据与目标曲线距离多远。R2越接近1表示模型的性能越好,越接近0则表示模型性能越差。
回归类模型的性能指标评价中主要采用RMSE(均方误差),偏差值较多时用MAE(平均绝对误差)较合适。因为使用RMSE评价模型的时候,假如只有一个数据与实际测量值存在大偏差,由于误差会乘以一个平方导致全组数据的RMSE值变大,那么对模型的评价也就变得非常低了。
多分类情况
刚才所讲的分类模型的性能指标限于模型用于把数据集归类到两个类别的时候。但稍微想想,应该知道分类的时候不应该总是两类。那么面对能将数据集归类到两类以上的多类分类(Multiclass Classification),我们应该采用什么样的评价指标呢?
在多类分类的情况下,全部类的平均值取法有两种:微平均和宏平均8,9。
微平均(Micro-average)……对所有类别的结果进行不加权的整体评估。跨类了解整体表现8。
宏平均(Macro-average)……当特定的数据很少或每个类的数据有偏差时,想要考虑数据偏差带来的影响时使用比较好8。
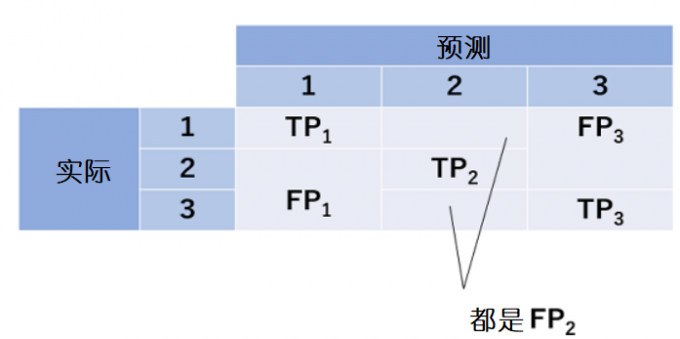
是混淆矩阵。各个级别的真阳性、假阳性用TP1、FP1来表示。TP1代表实际结果和预测都被归为1类的个数,FP1代表的是预测归为1类但实际不属于1类的个数。
我想从准确率的微平均值开始。
混淆矩阵中准确率的微平均值用如下公式表示。
接下来是准确率的宏平均值。
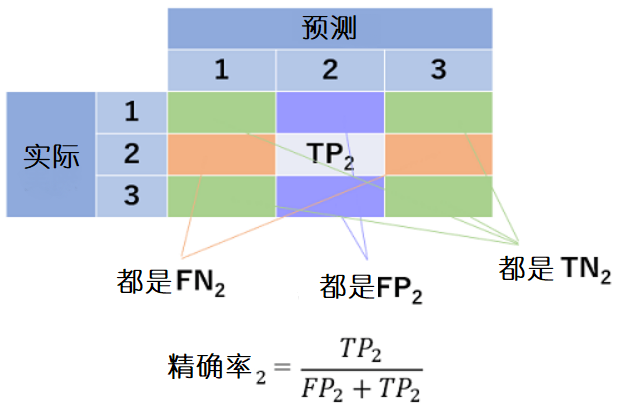
为了考虑各个类的准确率,制作3个混淆矩阵,并考虑各自的准确率。例如,着重关注第1类,然后将所有的类别划分为第1类或非第1类。
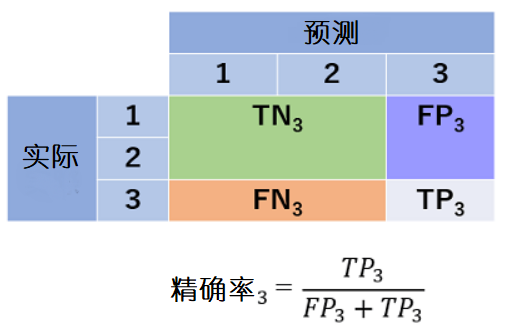
与其他类相加也是如此。
由各个类别准确率推导出准确率的宏平均值的公式如下所示。
如果类别再多,照此类推即可评价多分类模型的性能了10。
结束语
这次提出的模型性能指标不仅适用于化学专业·材料专业的机器学习,也适用于所有领域的机器学习。研究模型的性能评价都采用了哪些指标会非常得有意思。
参考文献
- 金子弘昌 著, Pythonで気軽に化学・化学工学, p. 147, 丸善出版, 2021
- 大曽根圭輔, 関喜史, 米田武 著, 現場で使える!Python機械学習入門, pp. 138-142, 翔泳社, 2019
- 大曽根圭輔, 関喜史, 米田武 著, 現場で使える!Python機械学習入門, p. 130, 翔泳社, 2019
- 金子弘昌 著, 化学のためのPythonによるデータ解析・機械学習入門, pp. 81-82, オーム社, 2019
- 島田達郎, 越水直人, 早川敦士, 山田育矢 著, Pythonによるはじめての機械学習プログラミング, p. 159, 技術評論社, 2019
- 下田倫大 監訳, scikit-learnとTensorFlowによる実践機械学習, pp. 37–39, オライリージャパン, 2018
- 堅田洋資, 菊田遥平, 谷田和章, 森本哲也 著, フリーライブラリで学ぶ機械学習入門, pp.37-38, 秀和システム, 2017
- 有賀康顕, 中山心太, 西林孝 著, 仕事で始める機械学習, pp. 65–75, オライリージャパン, 2018
- 中田秀基 訳, Pythonではじめる機械学習, pp. 292-295, オライリージャパン, 2017
- 福島真太朗 監訳, [第3版]Python機械学習プログラミング達人データサイエンティストによる理論と実践, p. 191, インプレス, 2020
- 金子弘昌 著, 化学のためのPythonによるデータ解析・機械学習入門, pp. 55-57, オーム社, 2019
- 下田倫大 監訳, scikit-learnとTensorFlowによる実践機械学習, pp. 86-89, オライリージャパン, 2018
本文版权属于 Chem-Station化学空间, 欢迎点击按钮分享,未经许可,谢绝转载







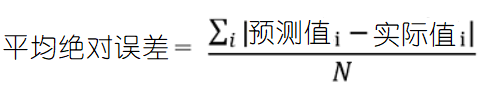
















No comments yet.