译自Chem-Station网站日本版 原文链接:誤解してない? 電子の軌道は”軌道”ではない
翻译:炸鸡 校对:Jiao Jiao
今天来带大家“盘”我们化学领域里一个十分重要的概念:轨道。在正式开始讲解之前,我想先解释清楚以下三个化学学习者通常会有的疑问。
- 微观量子世界和我们生活的普通世界到底有什么不同?(或者量子力学和牛顿经典力学之间有什么不同)
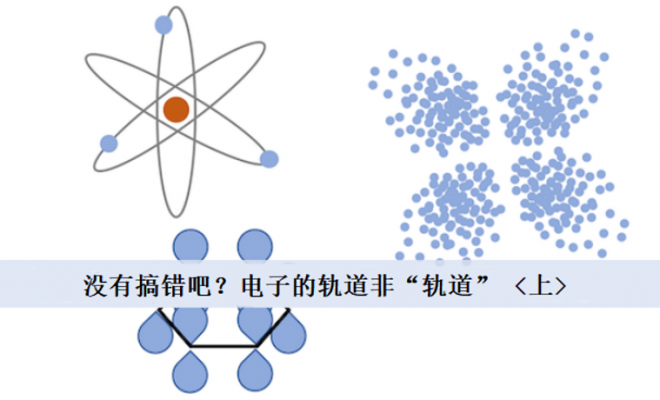
- 我们熟知的轨道如s轨道,p轨道,d轨道和字面意义上的“轨道”形状一致吗,这些原子轨道在空间上有着广泛的分布吗?
- 在思考原子的电子排布时,我们通常会表述为将电子填入轨道,但这背后揭示了轨道和电子之间怎样的关系呢?
疑问1的答案关键存在于光的波粒二象性里。疑问2和3甚至笔者我也曾迷惑了好久。疑问2和疑问3的答案在本篇记事里。今天我将从不同的视角揭开量子世界的迥异之处。
轨道可谓是学化学的一个必学概念了,无论你学的是化学的哪个分支学科,哪怕不是物理化学,首先学的也是轨道。现在有机系统的研究时也会不可避免地会用到s轨道,p轨道等(无机化学甚至会用到d轨道和f轨道)来分析一些定性的结果。现在轨道概念可以说已经渗透到了化学的各个角落,个人大言不惭的说这简直就是化学的三大神器!
作为化学领域最为重要的概念的轨道,却往往不太被重视。在化学相关的教科书和课堂上,往往展示完轨道的形状后就立马进入轨道的应用了。很多学生也就习惯了,想“嗯嗯,好的,我明白了”,然后接着往下学习。但是,越是基础简单的内容,如果深挖深思,就会发现有很多自己原本不明白的地方。我希望我的这篇文章能够给一些中级化学学习者们一些新的启迪,为一些预备复习基础知识的人解除他们学习道路上出现的种种困惑的根源,期望我的这篇文章能够为一部分人带来帮助。所以我将从最基础的层面开始讲起。
OK!废话不多说,让我们开始吧。
经典力学和量子力学到底差在哪?
首先我们从轨道概念的层面来一窥量子力学的世界。我们需要厘清经典力学和量子力学的决定性不同点。经典力学和量子力学的区别绝不是字面上一个旧一个新的意思。经典力学并不是已经被现代社会抛弃了,相反,在解释宏观世界的物理现象上,经典力学、电磁学等仍然是基本的纲领。但是在19世纪后半叶到20世纪前半叶这段时间内,用我们长期形成的传统思维方法,出现了很多无法解释的现象,所以那时的人们意识到理论需要一个重大变革。因为量子世界和我们普通人视野里的世界差异太大,所以量子力学的诞生是物理学史上的里程碑。
经典力学可以明确地描述物体的运动轨迹
我们初中和高中学习的物理统称为经典力学。经典力学的一大用处是预测运动的物体的运动状态。具体说是在知道物体的初始状态的情况下,用一个与时间有关的函数来表示物体的运动状态,这个运动函数描述了这个物体过去的以及将来的运动状态。通过运动函数可以知道物体的运动轨迹及其每个时间点的速度和加速度。
将物体的运动状态与时间建立联系的就是如下所示的牛顿第二定律方程。
F=ma (1)
如果对一个质量为m的物体施加一个力F,物体就会产生一个大小为a的加速度。像这样“某种原因产生某种结果”的思考模式被称为因果律。Newton自己在著作《自然哲学的数学原理》中写道:力的施加会导致“动量mv”发生变化。当然也需要考虑物体质量m的改变,这里暂且不论。
以上所述的牛顿第二定律对大家来说可谓是很熟悉了。但我希望大家能从牛顿方程里认识到两个准则。
- 在经典力学中,物体的轨迹可以根据牛顿第二定律和初始条件来确定。
- 加速度和速度等物理量可以根据方程算出,连同它们在这一刻的时间一起组成了这个物体在这一刻的全部物理量信息,不同时刻的物体的物理量信息都是不同的
第二点可能需要点解释:用位置x,速度v, 时间t来表示物体在某个位置某个时间的动量P,那么P1:(x1, v1, t1)=(2,3,1),P2:(x2, v2, t2)=(3,4,2),因为物体不同时刻的加速度和速度都是不同的,所以可以判断P1≠P2。
在量子力学里,电子在任一时刻的位置是不确定的[1]
上述提到的在经典力学里成立的两条准则在量子世界里一般是不成立的。对于准则一“在经典力学中,物体的轨迹可以根据牛顿方程式和初始条件来确定”,就日常生活经验来理解也是很容易的,比如我们日常生活中的几乎所有的物体都有一个确定的运动轨迹,预测一个确定的运动轨迹并不是难事。
如果我们拿起书桌上的一块橡皮移动下它,在这个移动的过程里这个橡皮会有一个肉眼可见的运动轨迹(橡皮不会突然消失在某处又突然出现在某处)。有的运动速度很快的物体可以用闪频仪捕捉到运动轨迹,总之都可以很好地确定运动轨迹。但是在量子世界里我们就要舍弃“轨迹”这一在经典力学里习以为常的概念。
- 电子各时刻的位置是不确定的,无法追踪电子的运动轨迹
这听起来简直不可思议。如果连电子的确切位置都无从所知,到底该从哪里着手考虑呢?电子确切位置的不明朗带来更多的变数。
- 在量子世界里通常准确给出全部的物理量的数值是不可能的。也就是说在测量某个物理量时都会产生一定的偏差
具体怎么测量其实也挺困难的。想要了解怎么测量量子世界里的物理量的读者可以自行阅读量子测量的相关书籍。读懂这篇文章不需要详细理解量子测量手段,只需要知道怎么测量位置和动量就足够了。
毫无疑问这对习惯于经典力学的我们来说是一种冲击。如果你不知道轨迹,你就不能同时确定物理量。而且求解量子世界里的物理量时不可避免会有误差,这个误差竟然还不是人为的,是事物与生俱来的!
清楚且深刻的理解以上两点在量子化学学习中十分重要,但可惜现在很少有教材能浓墨重彩地指出这两点而是将重点过度地放在文章开头所说的光的波粒二象性上。光的波粒二象性很可能会给初学者埋下困惑,比较适合学习了一段量子力学并且已经复习过量子力学的人。我个人认为初学者或学习量子化学有困难的人只要清楚地认识并且深刻学习以上两点就会有助于理解量子化学,也会更好地把量子力学与化学在脑海里建立起联系。
讲到这里可能会有聪明的读者猜到量子世界里的“不确定”性与今天的主题原子轨道之间的关联了吧。我们虽然称呼原子轨道是s轨道,p轨道,d轨道…这些所谓的“轨道”都属于量子概念,应当区别于经典力学甚至我们日常生活认知里对轨道的固有概念。
但是因为翻译的原因,“轨道”一词一直深入人心,让初学者甚至学了好一段时间的人产生混乱。请务必记在心里:它说是说轨道,但它实际上又不是轨道。下面让我们深入讲解。
原子轨道的推导过程
首先让我复习下轨道是怎么产生的。
让我们请出在量子力学界的地位堪比牛顿第二定律在经典力学里的地位的Schrödinger方程(薛定谔方程)!
(2)
请注意,准确来说上述表达式并不是Schrödinger方程,而是满足正交关系的哈密顿算符的Schrödinger表达式。虽然Schrödinger方程和Schrödinger表达式之间存在明显的差异,但由于许多教科书将表达式(2)称为Schrödinger方程,因此为了避免混淆,我们将在此对其进行调整。下面的(3)是包含了哈密顿算符但不含时间的Schrödinger表达式。
(3)
这就是定态Schrödinger方程。想要详细了解定态Schrödinger方程的读者感兴趣可以参考化学空间的《再次走进薛定谔方程!:定态和变量分离》。我们现在谈论的Schrödinger方程,关于时间的Schrödinger方程就像一部电影,而定态Schrödinger方程就像一帧照片(在一个时间T内不变),一帧帧照片快速播放就构成了一部电影。
现在,我们手握Schrödinger方程表达式和定态Schrödinger方程,我们可以推导出另一种形式的Schrödinger方程了——单个电子在受到库仑力下的电子的Schrödinger方程。详细过程这里不赘述,感兴趣的读者可以查阅相关书籍。
(4)
表示粒子位置的坐标系会根据待研究的系统而做调整。比如研究只受到一个中心力的粒子,极坐标系就比较合适。
~未完待续~
参考文献
[1]清水明, 第1章 古典物理学の破綻 第2章 基本的枠組み「新版 量子論の基礎」サイエンス社, 2018年, pp10-14, 19-21.本文版权属于 Chem-Station化学空间, 欢迎点击按钮分享,未经许可,谢绝转载

















No comments yet.