译自Chem-Station网站日本版 原文链接:計算化学:DFT計算って何?Part II
翻译:炸鸡
近年来,用DFT计算结果来佐证实验结果和实验结论的论文越来越多了。很多实验化学研究人员也越来重视计算化学知识的学习。
但是很少有实验化学研究人员真正深入理解DFT。尽管很多实验化学研究者都或多或少地会DFT计算操作,但很少有人真正会刨根问底地问:“到底什么是DFT计算?”
我虽然没有胆大到问周围的人“你知道什么是DFT计算吗?”,但在某个深夜我还是悄咪咪地打开某百科网站,但发现DFT的解释只停留在了“密度泛函理论”这几个字上。能用简洁易懂的大白话解释DFT的网络文章或教科书基本很少很少。我个人认为计算化学如此小众的原因不仅在于这门学科本身的难度大,还在于没有一本简洁易懂的好教材。
作为《计算化学的一点简单科普》系列,延续前两回的任务,将继续向新手小白提供一点计算化学的入门小知识。今天这篇推文将从量子化学计算的“诞生”说起,让即使是初学者小白也能明白何为DFT计算。
量子力学的发展

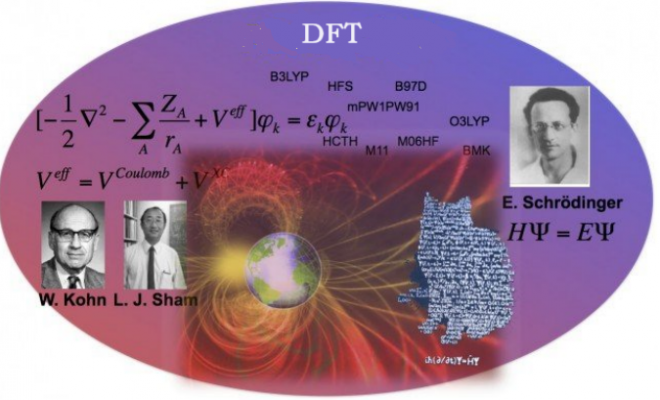
基于“如果知道某个物质的电子状态就能预测这个化合物的性质和反应特性”这个大胆的想法,有机化学家们便踏上了量子化学计算的道路。渐渐地,一位叫薛定谔的物理学家发现了薛定谔方程,只要解出这个薛定谔方程,咱们就能知道物质的电子状态了。
薛定谔方程于1926年被提出。之后又有一位物理学家保罗·狄拉克将相对论融合进了薛定谔方程中,在1928年提出了狄拉克方程。
上世纪20至30年代堪称量子力学发展的黄金时期,哈特里法(Hartree 法)(1928年Hartree)、斯莱特行列式(Slater determinant)(1929年Slater)、哈特里-福克方程(Hartree–Fock equation)(1930年Fock, Slater)、分子轨道法(1926年Hund、1927年Mulliken)、Møller-Plesset 法(MP2法)(1934年Moller, Plesset)、TDHF法(1930年Dirac)LDA交换泛函(1930年Dirac)等等,许多理论犹如雨后春笋般冒出来,数不胜数。这段黄金时期冒出的理论都只有一个终极目标——“如何解出实际存在的分子的薛定谔方程?”
说句题外话,保罗·狄拉克真是个了不起的人。他在提出和发展各种理论方面做出了巨大贡献。关于他因为“不想变得太有名”而试图拒绝诺贝尔奖,最终被周围的人全力阻止的故事,确实有点独特。他真的是一个了不起的人物。
随后,物理学家和化学学家又在围绕着“如何描绘出分子中的电子运动的波函数”这一问题展开攻坚。杂化轨道模型(1928年Pauling)、过渡态理论(1935年Eyring)、LCMO近似(1929年Lennard-Jones、1938年Coulson)、化学反应原理(1936年Bell、1938年Evans, Polanyi)等理论相继被发表。
这么多化学家前仆后继地提出了这么多理论,终极目标只有一个——求得薛定谔方程的解。然而,严密准确求解薛定谔方程是不可能的,于是求得薛定谔方程的近似解渐渐变成了新的任务,于是化学家们的努力方向从精确求解到求近似解,围绕如何求得近似解的理论在1930年前后引来了井喷式成长。
DFT(密度泛函理论)的发展历史
上面介绍的一大堆理论都是在探讨怎么求得薛定谔方程的近似解。但DFT却偏不这么干,它高喊着“我要努力求得哈密顿算符”,它走上了一条另类的道路。

作为DFT的基础理论的Thomas-Fermi理论于1927年被提出。这个理论简单用一句话来概括就是“只用电子密度便可将哈密顿算符表示出来”。
但是在早期,Thomas-Fermi理论缺乏物理证据保证解的唯一性或证明泛函的存在,甚至无法准确再现化学键。所以在1960年之前Thomas-Fermi理论一直坐冷板凳。现在计算化学家们推崇的DFT在当年也是被大众嫌弃的存在。
到了1964年,DFT的命运开始迎来转机,能为Thomas-Fermi理论提供物理证据的理论——Hohenberg-Kohn定理出现了。Hohenberg-Kohn定理是从下面两个定理得出来的:
- 外场的势能是由电子密度决定的。
- 对于所有的电子密度,能量的变分原理都成立。
Kohn-Sham 方程
在《计算化学的一点简单科普(1):什么是泛函?》中,Kohn-Sham方程的登场方式可能有点突然,今天我来正式介绍Kohn-Sham方程。

Hohenberg-Kohn定理的出现证明了Thomas-Fermi理论的正确性,然而实际的电子状态计算不出。以Thomas-Fermi理论为基础的计算方法等到1965年Kohn-Sham方程的提出才被人接受。
Kohn-Sham方程在计算运能时,不再使用电子密度的泛函,而是采用了一种与Hartree-Fock方法相似的独立粒子近似的方法,用于计算多电子体系中的动能。在这个方法中,不再使用电子密度的泛函,而是采用了更为简化的处理方式。凭借着Kohn-Sham方程,化学·固体物理性质的定量计算成为了可能,DFT借此迎来了“职业道路”的飞升。
因为有了Kohn-Sham方程的注解,现在广泛使用的DFT计算其实和当初Thomas-Fermi理论提出的DFT计算方法有较大出入。很多人不知道的是,DFT理论并不完全等于Kohn-Sham方程。
总结下DFT理论发展的时间线:
1927年DFT理论被提出→被当时的科学家认为没啥大用处→1964年Hohenberg-Kohn定理为DFT理论背了书→1965年Kohn-Sham方程被提出,DFT理论终于可以用于实际计算了
1930年到1980年之间量子化学的进展就讲完了,量子化学之后还有哪些发展呢?敬请期待下回分解。
本文版权属于 Chem-Station化学空间, 欢迎点击按钮分享,未经许可,谢绝转载.
























No comments yet.